Câu hỏi/bài tập:

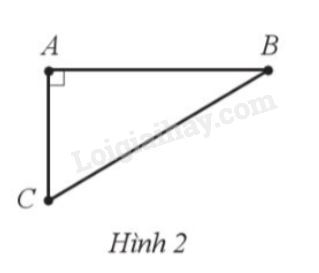
Hàng ngày, hai anh em An và Bình cùng đi bộ từ nhà ở vị trí A đến trường. Trường của anh An ở vị trí B và trường của em Bình ở vị trí C theo hai hướng vuông góc với nhau (Hình 2). Anh An đi với tốc độ 4 km/h và đến trưởng sau 15 phút. Em Bình đi với tốc độ 3 km/h và đến trường sau 12 phút. Tính khoảng cách BC giữa hai trường (làm tròn kết quả đến hàng phần trăm của mét).

Bước 1: Áp dụng công thức \(s = v.t\) để tính quãng đường AB,AC.
Bước 2: Áp dụng định lý Pythagore trong tam giác vuông ABC để tính BC.
Advertisements (Quảng cáo)

Đổi 15 phút = 0,25 giờ; 12 phút = 0,2 giờ.
Quãng đường AB là \(4.0,25 = 1\left( {km} \right).\)
Quãng đường AC là \(3.0,2 = 0,6\left( {km} \right).\)
Áp dụng định lý Pythagore trong tam giác vuông ABC ta có:
\(C{B^2} = A{B^2} + A{C^2} = {1^2} + 0,{6^2} = 1,36\), do đó \(CB = \sqrt {1,36} \) hay \(CB \approx 1,17\)km.
Vậy khoảng cách BC giữa hai trường khoảng 1,17km.
