Câu hỏi/bài tập:

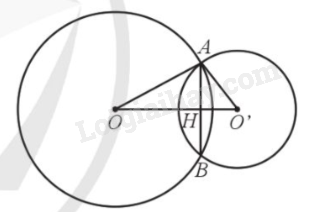
Cho hai đường tròn (O; 17cm) và (O’; 10cm) cắt nhau tại A và B. Biết OO’ = 21cm. Tính độ dài đoạn thẳng AB.

Bước 1: Chứng minh OO’ là đường trung trực của AB, từ đó suy ra \(AH = BH = \frac{{AB}}{2}\) .
Bước 2: Tính \(O’H = OO’ - OH = 21 - OH\).
Bước 3: Áp dụng định lý Pythagore trong tam giác vuông AOH và O’AH để biểu diễn AH thông qua OH và tính OH.
Bước 4: Tính \(AB = 2AH\).

Advertisements (Quảng cáo)
Gọi H là giao điểm của OO’ và AB.
Ta có: \(OA = OB( = 17cm)\)nên O thuộc đường trung trực của AB;
\(O’A = O’B( = 10cm)\) nên O’ thuộc đường trung trực của AB.
Suy ra OO’ là đường trung trực của AB, do đó \(AH = BH = \frac{{AB}}{2}\) và \(OO’ \bot AB\) tại H.
Ta có \(O’H = OO’ - OH = 21 - OH\)
Mặt khác: Áp dụng định lý Pythagore trong tam giác vuông AOH và O’AH ta được:
\(O{A^2} - O{H^2} = O'{A^2} - O'{H^2}( = A{H^2})\)
Nên \({17^2} - O{H^2} = {10^2} - {\left( {21 - OH} \right)^2}\) hay \({17^2} - O{H^2} = {10^2} - \left( {{{21}^2} - 42OH + O{H^2}} \right)\) do đó \(OH = 15\)cm.
Áp dụng định lý Pythagore trong tam giác vuông OAH ta có: \(AH = \sqrt {O{A^2} - O{H^2}} = \sqrt {{{17}^2} - {{15}^2}} = 8\)cm.
Vậy \(AB = 2AH = 2.8 = 16\)cm.
