Câu hỏi/bài tập:

Cho hình chữ nhật ABCD với AB = 10cm. Vẽ hai nửa đường tròn tâm O đường kính AB và tâm O’ đường kính CD cắt nhau tại P, Q. Biết rằng đường tròn tâm H đường kính PQ tiếp xúc với AB và CD (Hình 47). Tính diện tích phần chung của hai nửa đường tròn (O), (O’).
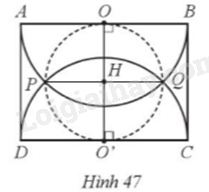

Bước 1: Chứng minh OPO’Q là hình vuông và cạnh hình vuông.
Bước 2: Diện tích cần tìm = diện tích phần tạo bởi dây PQ và cung nhỏ PQ của (O) + diện tích phần tạo bởi dây PQ và cung nhỏ PQ của (O’).
Trong đó:
Diện tích phần tạo bởi dây PQ và cung nhỏ PQ của (O) = diện tích quạt tròn OPQ – diện tích tam giác OPQ.
Diện tích phần tạo bởi dây PQ và cung nhỏ PQ của (O’) = diện tích quạt tròn O’PQ – diện tích tam giác O’PQ.

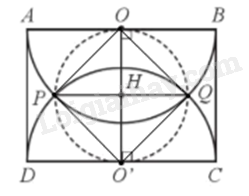
Ta có: O là tâm đường tròn đường kính AB nên \(OA = OB = OP = OQ = \frac{{AB}}{2} = \frac{{10}}{2} = 5\)cm.
Ta lại có: O’ là tâm đường tròn đường kính CD nên \(O’C = O’D = O’P = O’Q = \frac{{CD}}{2}\)
Mà \(AB = CD\) (do ABCD là hình chữ nhật), suy ra \(OP = OQ = O’P = O’Q\).
Advertisements (Quảng cáo)
Có: AB, CD tiếp xúc với (H), \(OH \bot AB\)tại O tại O’, do đó O và O’ là tiếp điểm của 2 tiếp tuyến AB và CD của (H), hay \(O \in (H),O’ \in (H)\).
Diện tích tam giác OPQ là:
\(\frac{1}{2}OP.OQ = \frac{1}{2}5.5 = \frac{{25}}{2}\)(cm2)
Diện tích hình quạt tròn OPQ của (O) là
\(\frac{{\pi {{.5}^2}.90}}{{360}} = \frac{{25\pi }}{4}\)(cm2)
Diện tích hình tạo bởi dây PQ và cung nhỏ PQ của (O) là:
\(\frac{{25\pi }}{4} - \frac{{25}}{2} = \frac{{25}}{4}\left( {\pi - 2} \right)\)(cm2)
Diện tích tam giác O’PQ là:
\(\frac{1}{2}OP.OQ = \frac{1}{2}5.5 = \frac{{25}}{2}\)(cm2)
Diện tích hình quạt tròn O’PQ của (O’) là
\(\frac{{\pi {{.5}^2}.90}}{{360}} = \frac{{25\pi }}{4}\) (cm2)
Diện tích hình tạo bởi dây PQ và cung nhỏ PQ của (O’) là:
\(\frac{{25\pi }}{4} - \frac{{25}}{2} = \frac{{25}}{4}\left( {\pi - 2} \right)\) (cm2)
Vậy diện tích phần chung của 2 nửa đường tròn (O) và (O’) là:
\(2.\frac{{25}}{4}\left( {\pi - 2} \right) = \frac{{25}}{2}\left( {\pi - 2} \right)\) (cm2)
