Câu hỏi/bài tập:

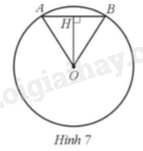
Hình 7 mô tả công trình xây dựng cây cầu bắc qua một hồ nước với mặt hồ có dạng hình tròn tâm O bán kính 2 km. Cây cầu có hai đầu cầu là hai điểm A, B nằm trên đường tròn tâm O. Tính chiều dài của cây cầu để khoảng cách từ tâm O của hồ nước đến cây cầu là OH = 1732 m (làm tròn kết quả đến hàng đơn vị của mét).

Bước 1: Áp dụng định lý Pythagore trong tam giác vuông AHO để tính AH.
Bước 2: Chứng minh AH = BH.
Bước 3: Tính AB = 2AH.

Advertisements (Quảng cáo)
Ta có \(OA = OB = 2km = 2000m,OH = 1732m\).
Áp dụng định lý Pythagore trong tam giác vuông AHO ta có:
\(AH = \sqrt {A{O^2} - O{H^2}} = \sqrt {{{2000}^2} - {{1732}^2}} = \sqrt {1000176} m.\)
Xét 2 tam giác vuông AHO và BHO ta có:
\(AO = BO( = R)\);
HO chung
Suy ra \(\Delta AHO = \Delta BHO\) (cạnh huyền – cạnh góc vuông) nên AH = BH.
Vậy \(AB = AH + BH = 2AH = 2\sqrt {1000176} \approx 2000m.\)
