Áp dụng tỉ số lượng giác \(\tan \widehat {BCA} = \frac{{AB}}{{AC}}\), từ đó tính được số đo góc BCA. Trả lời Giải bài 7 trang 82 sách bài tập toán 9 - Cánh diều tập 1 - Bài 1. Tỉ số lượng giác của góc nhọn . Một đài quan sát không lưu có độ cao là AB = 95 m.
Câu hỏi/bài tập:

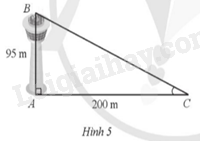
Một đài quan sát không lưu có độ cao là AB = 95 m. Ở một thời điểm nào đó vào ban ngày, Mặt Trời chiếu tạo bóng dài AC = 200 m trên mặt đất. Góc tạo bởi tia sáng Mặt Trời và phương nằm ngang là góc BCA (Hình 5). Tính số đo góc BCA (làm tròn kết quả đến hàng đơn vị của độ).

Advertisements (Quảng cáo)
Áp dụng tỉ số lượng giác \(\tan \widehat {BCA} = \frac{{AB}}{{AC}}\), từ đó tính được số đo góc BCA.

Xét tam giác ABC vuông tại A ta có:
\(\tan \widehat {BCA} = \frac{{AB}}{{AC}} = \frac{{95}}{{200}} = \frac{{19}}{{40}}\)
Suy ra \(\widehat {BCA} \approx 25^\circ \).
