Câu hỏi/bài tập:

Cho Hình 6 có AB = 3 cm, CD = 4 cm. Tính số đo góc AOC (làm tròn kết quả đến hàng đơn vị của độ).
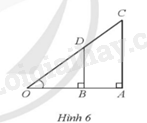

Bước 1: Chứng minh \(BD//CA\), sau đó áp dụng định lý Thales để suy ra \(\frac{{OA}}{{OB}} = \frac{{OC}}{{OD}}\).
Bước 2: Áp dụng tính chất dãy tỉ số bằng nhau: \(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{OA - OB}}{{OC - OD}} = \frac{{AB}}{{CD}} = \frac{3}{4}\)
Advertisements (Quảng cáo)
Bước 3: \(\cos \widehat {AOC} = \frac{{OA}}{{OC}}\), từ đó suy ra số đo góc AOC.

Ta có: \(BD \bot OA,CA \bot OA\) nên \(BD//CA\).
Xét tam giác OAC có \(BD//CA\), áp dụng định lý Thales, ta được: \(\frac{{OA}}{{OB}} = \frac{{OC}}{{OD}}\)
Suy ra \(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{OA - OB}}{{OC - OD}} = \frac{{AB}}{{CD}} = \frac{3}{4}\)
Vì tam giác OAC vuông tại A nên ta có \(\cos \widehat {AOC} = \frac{{OA}}{{OC}} = \frac{3}{4}\), do đó \(\widehat {AOC} \approx 41^\circ \).
