
Cho tam giác OAB vuông tại O có OA = 8 cm, OB = 15 cm.
a) \(\tan A = \frac{{15}}{8}\)
b) \(\sin B = \frac{{15}}{{17}}\)
c) \(\sin A = \frac{8}{{17}}\)
d) cot A = tan B

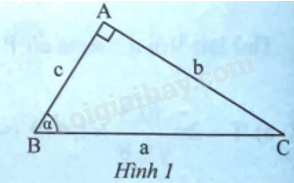
Dựa vào: Tam giác vuông ABC trong Hình 1, ta có:
\(\sin \alpha = \frac{{AC}}{{BC}} = \frac{b}{a};\cos \alpha = \frac{{AB}}{{BC}} = \frac{c}{a};\tan \alpha = \frac{{AC}}{{AB}} = \frac{b}{c};\cot \alpha = \frac{{AB}}{{AC}} = \frac{c}{b}.\)
Advertisements (Quảng cáo)
Chú ý: Với góc nhọn \(\alpha \), ta có:
0
cot \(\alpha \) = \(\frac{1}{{\tan \alpha }}\)

a) Đúng vì \(\tan A = \frac{{OB}}{{OA}} = \frac{{15}}{8}\).
b) Sai vì \(AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{8^2} + {{15}^2}} = 17\)
Suy ra sin B = \(\frac{{OA}}{{AB}} = \frac{8}{{17}}\).
c) Sai vì sin A = \(\frac{{OB}}{{AB}} = \frac{{15}}{{17}}\).
d) Đúng vì cot A = \(\frac{{OA}}{{OB}} = \frac{8}{{15}}\) và tan B = \(\frac{{OA}}{{OB}} = \frac{8}{{15}}\).
