Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng. Hướng dẫn trả lời - Bài 11 trang 74 sách bài tập toán 9 - Chân trời sáng tạo tập 1 - Bài tập cuối chương 4. Tam giác ABC vuông tại A, có AB = 24 cm, BC = 25 cm, AH là đường cao (Hình 5). a) AC = 8 cm b) (widehat B approx {16, 26^o}) c) ({rm{cosC = }}frac{{24}}{{25}}) D...

Tam giác ABC vuông tại A, có AB = 24 cm, BC = 25 cm, AH là đường cao (Hình 5).
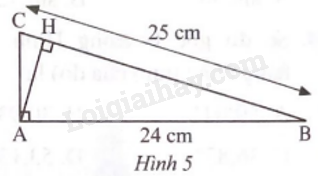
a) AC = 8 cm
b) \(\widehat B \approx {16,26^o}\)
c) \({\rm{cosC = }}\frac{{24}}{{25}}\)
D. \(AH \approx 7\)
Advertisements (Quảng cáo)

Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.

a) Sai vì AC = \(\sqrt {B{C^2} - A{B^2}} = \sqrt {{{25}^2} - {{24}^2}} = 7\).
b) Đúng vì \(\tan B = \frac{{AC}}{{AB}} = \frac{7}{{24}}\) suy ra \(\widehat B \approx {16,26^o}\).
c) Sai vì \({\rm{cosC = }}\frac{{AC}}{{BC}} = \frac{7}{{25}}\).
d) Đúng vì AH = tan B. AB = \(\frac{7}{{24}}.\)24 = 7 cm.
