
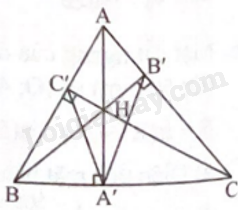
Cho tam giác ABC nhọn với các đường cao AA’, BB’, CC’. Chứng minh rằng A’A là tia phân giác của góc \(\widehat {B’A’C’}\).

Chứng minh bốn điểm B, A’, H, C’ cùng nằm trên một đường tròn
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

Advertisements (Quảng cáo)
Gọi H là trực tâm của tam giác ABC.
Ta có \(\widehat {BC’H} = \widehat {BA’H} = {90^o}\), nên bốn điểm B, A’, H, C’ cùng nằm trên một đường tròn.
Do đó \(\widehat {HA’C’} = \widehat {HBC’}\).
Chứng minh tương tự, ta cũng có \(\widehat {HA’B’} = \widehat {HCB’}\).
Mà \(\widehat {HBC’} = \widehat {HCB’}\) (cùng phụ với \(\widehat {BAC}\)), nên ta có \(\widehat {C’A’H} = \widehat {B’A’H}\).
Từ đó, ta có A’A là tia phân giác của góc \(\widehat {B’A’C’}\).
