
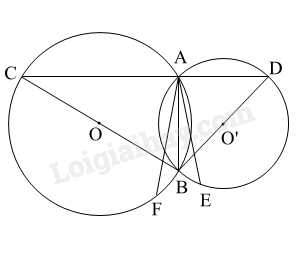
Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại hai điểm A và B phân biệt. Vẽ đường thẳng vuông góc với AB tại A và cắt (O), (O’) lần lượt tại C, D. Tia CB cắt (O’) tại E, tia DB cắt (O) tại F. Chứng minh rằng:
a) CD.CA = CB.CE.
b) DC.DA = DB.DF.
c) CD2 = CB.CE + DB.DF.

Dựa vào: Hai góc nội tiếp cùng chắn một cung thì bằng nhau
Góc nội tiếp bằng nửa số đo cung bị chắn.

Advertisements (Quảng cáo)
a) Xét tam giác CDB và tam giác CEA có góc C chung. Trong đường tròn (O’), ta có:
\(\widehat{CDB}=\widehat{ADB}=\frac{1}{2}sđ\overset\frown{AB}\),
\(\widehat{CEA}=\widehat{BEA}=\frac{1}{2}sđ\overset\frown{AB}\)
Suy ra \(\widehat {CDB} = \widehat {CEA}\), do đó \(\Delta CDB\backsim \Delta CEA\)
Suy ra \(\frac{{CD}}{{CE}} = \frac{{CB}}{{CA}}\) hay CD.CA = CB.CE.
b) Chứng minh tương tự, ta cũng có DC.DA = DB.DF.
c) Ta có:
CB.CE + DB.DF = CD.CA + DC.DA = CD(CA + AD) = CD.CD = CD2.
