
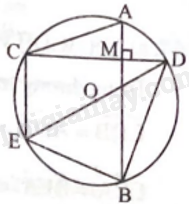
Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau (D thuộc cung nhỏ AB). Vẽ đường kính DE. Chứng minh:
a) MA.MB = MC.MD.
b) Tứ giác ABEC là hình thang cân.
c) Tổng MA2 + MB2 + MC2 + MD2 có giá trị không đổi khi M thay đổi vị trí trong đường tròn (O).

Dựa vào: Hai góc nội tiếp cùng chắn một cung thì bằng nhau.
Chứng minh ABEC là hình thang. Sau đó chứng minh \(\widehat {EBA} = \widehat {CAB}\) để ABEC là hình thang cân.
Chứng minh tổng MA2 + MB2 + MC2 + MD2 theo R.

Advertisements (Quảng cáo)
a) Xét \(\Delta \)MAC và \(\Delta \)MDB, ta có \(\widehat{AMC}=\widehat{DMB}={{90}^{o}},\widehat{ACM}=\widehat{DMB}\left( \frac{1}{2}sđ\overset\frown{AD} \right).\)
Do đó \(\Delta \)MAC \(\backsim \) \(\Delta \)MDB, suy ra \(\frac{{MA}}{{MD}} = \frac{{MC}}{{MB}}\) hay MA.MB = MC.MD.
b) Vì DE là đường kính nên ta có \(CE \bot CD\).
Mà \(AB \bot CD\) nên AB // CE, suy ra ABEC là hình thang.
Ta có \(\widehat {EBA} + \widehat {MBD} = {90^o};\widehat {CAB} + \widehat {ACM} = {90^o};\widehat {ACM} = \widehat {DMB}\), suy ra \(\widehat {EBA} = \widehat {CAB}\). Vậy ABEC là hình thang cân.
c) Ta có AC = BE (vì ABEC là hình thang cân) và \(\Delta DBE\)vuông tại B, nên ta có
MA2 + MB2 + MC2 + MD2 = AC2 + BD2 = BE2 + BD2 = ED2 = 4R2.
Vậy tổng MA2 + MB2 + MC2 + MD2 có giá trị không đổi.
