Bài 7 trang 73 SBT Toán 9 - Chân trời sáng tạo tập 1: Khoảng cách giữa hai chân tháp AB và MN là x (Hình 3). So với phương nằm ngang AH...

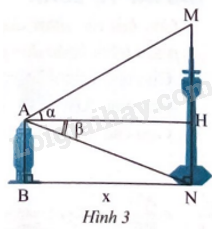
Khoảng cách giữa hai chân tháp AB và MN là x (Hình 3). So với phương nằm ngang AH, từ đỉnh A của tháp AB nhìn lên đỉnh M của tháp MN ta được góc \(\alpha \), từ đỉnh A của tháp AB nhìn xuống chân N của tháp MN ta được góc \(\beta \). Cho biết x = 120 m, \(\alpha \) = 30^o và \(\beta \) = 20^o . Chiều cao của tháp MN (kết quả làm tròn đến hàng đơn vị của mét) là

A. 113 m

B. 25 m

C. 101 m

D. 21,7 m

Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.

Ta có AH = BN = 120 m

tan \(\alpha = \frac{{MH}}{{AH}}\), suy ra MH = tan \(\alpha .AH = \tan {30^o}.120 = 40\sqrt 3 (m)\).

tan \(\beta = \frac{{NH}}{{AH}}\) suy ra NH = tan \(\beta .AH = \tan {20^o}.120 \approx 43,7(m)\).

Vậy MN = MH + NH \( \approx 40\sqrt 3 + 43,7 \approx 113\) m.

Chọn đáp án A.