
Hai trụ điện cùng chiều cao được dựng thẳng đứng ở hai bên lề đối diện một đại lộ rộng 80 m (AC = 80 m). Từ một điểm M trên mặt đường giữa hai trụ người ta nhìn thấy đỉnh hai trụ điện với các góc nâng lần lượt là 60o và 30o. Tính chiều cao của trụ điện và khoảng cách từ điểm M đến gốc mỗi trụ điện.
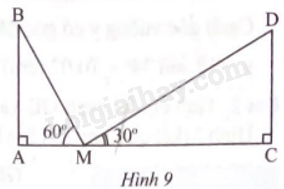

Sử dụng tỉ số lượng giác trong tam giác vuông để tính.

Xét tam giác ABM vuông tại A, ta có: \(\cot \widehat {AMB} = \frac{{AM}}{{AB}}\), suy ra AM = AB. \(\cot \widehat {AMB}\).
Xét tam giác CMD vuông tại C, ta có: \(\cot \widehat {CMB} = \frac{{CM}}{{CD}}\), suy ra CM = CD. \(\cot \widehat {CMB}\)
= AB. \(\cot \widehat {CMB}\).
Advertisements (Quảng cáo)
Ta có AC = AM + CM
80 = AB. cot 60o + AB. cot 30o
80 = AB (cot 60o + cot 30o)
AB = \(\frac{{80}}{{\cot {{60}^o} + \cot {{30}^o}}} = 20\sqrt 3 \).
Khoảng cách từ điểm M đến trụ điện AB là:
\(AM = AB.\cot \widehat {AMB} = 20\sqrt 3 .\frac{{\sqrt 3 }}{3} = 20(m).\)
Khoảng cách từ điểm M đến trụ điện CD là:
MC = AC – AM = 80 – 20 = 60 (m).
