a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số sau:
y = x (1)
y = 0,5x (2)
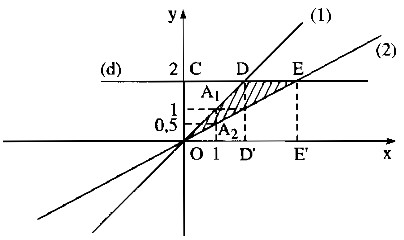
b) Đường thẳng (d) song song với trục Ox và cắt trục tung Oy tại điểm C
có tung độ bằng 2, theo thứ tự cắt các đường thẳng (1) và (2) tại D và E.
Tìm tọa độ của các điểm D, E . Tính chu vi và diện tích của tam giáo ODE.

a) * Vẽ đồ thị hàm số y = x
Cho x = 0 thì y = 0. Ta có : O(0;0)
Cho x = 1 thì y = 1. Ta có: A(1;1)
Đồ thị hàm số y = x đi qua O và A.
* Vẽ đồ thị hàm số y = 0,5x
Cho x = 0 thì y = 0.Ta có : O(0;0)
Cho x = 2 thì y = 1. Ta có : B(2;1)
Đồ thị hàm số y = 0,5x đi qua O và B .
b) Qua điểm C trên trục tung có tung độ bằng 2, kẻ đường thẳng song song với Ox
cắt đồ thị hàm số y = x tại D , cắt đồ thị hàm số y = 0,5x tại E.
Advertisements (Quảng cáo)
Điểm D có tung độ bằng 2.
Thay giá trị y = 2 vào hàm số y = x ta được x = 2
Vậy điểm D(2;2)
Điểm E có tung độ bằng 2.
Thay giá trị y = 2 vào hàm số y = 0,5x ta được x = 4.
Vậy điểm E(4;2)
Gọi D’ và E’ lần lượt là hình chiều của D và E trên Ox.
Ta có: OD’ = 2, OE’ = 4.
Áp dụng định lý Pi-ta-go vào tam giác vuông ODD’, ta có:
\(O{D^2} = OD{‘^2} + {\rm{DD}}{‘^2} = {2^2} + {2^2} = 8\)
Suy ra: \(OD = \sqrt 8 = 2\sqrt 2 \)
Áp dụng định lý Pi-ta-go vào tam giác vuông OEE’, ta có:
\(O{E^2} = OE{‘^2}{\rm{ + EE}}{{\rm{‘}}^2} = {4^2} + {2^2} = 20\)
Suy ra: \(OE = \sqrt {20} = 2\sqrt 5 \)
Lại có: \(DE = CE - CD = 4 - 2 = 2\)
Chu vi tam giác ODE bằng:
\(\eqalign{
& OD + DE + EO \cr
& = 2\sqrt 2 + 2 + 2\sqrt 2 \cr
& = 2\left( {\sqrt 2 + 1 + \sqrt 5 } \right) \cr} \)
Diện tích tam giác ODE bằng: \({1 \over 2}DE.OC = {1 \over 2}.2.2 = 2\)
