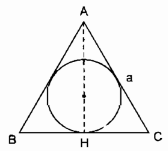
Cho hình quay một vòng xung quanh đường cao AH của tam giác đó, (xem hình 104), ta được một hình nón ngoại tiếp một hình nón ngoại tiếp hình cầu. Tính thể tích phần hình nón bên ngoài hình cầu.
 :
:
Gọi h là đường cao của tam giác đều, r là bán kính của đường tròn nội tiếp tam giác đó
Trong \(\Delta \) AHC có \(\widehat {AHC}\) = 90°; \(\widehat C\) = 60°
\(AH = AC.\sin C = a.\sin {60^{^0}} = {{a\sqrt 3 } \over 2}\)
\(\Delta \) ABC đều, tâm của đường tròn nội tiếp là giao điểm của ba đường phân giác đồng thời là đường trung tuyến là trung trực nên ta có:
Advertisements (Quảng cáo)
\(r = {1 \over 3}h = {{a\sqrt 3 } \over 6}\)
Thể tích hình nón:
\({V_1} = {1 \over 3}\pi .B{H^{^2}}.AH = {1 \over 3}\pi {\left( {{a \over 2}} \right)^2}.{{a\sqrt 3 } \over 2} = {{\pi {a^3}\sqrt 3 } \over {24}}\) (đơn vị thể tích)
Thể tích hình cầu:
\({V_2} = {4 \over 3}\pi {r^3} = {4 \over 3}\pi .{\left( {{{a\sqrt 3 } \over 6}} \right)^3} = {4 \over 3}\pi .{{3{a^3}\sqrt 3 } \over {216}} = {{\pi {a^3}\sqrt 3 } \over {54}}\)
Phần thể tích hình nón nằm ngoài hình cầu:
\({{\pi {a^3}\sqrt 3 } \over {24}} - {{\pi {a^3}\sqrt 3 } \over {54}} = {{9\pi {a^3}\sqrt 3 - 4\pi {a^3}\sqrt 3 } \over {216}} = {{5\pi {a^3}\sqrt 3 } \over {216}}\) (đơn vị thể tích)
