Cho hai đường tròn (O) và (O’) cắt nhau tại A và B, OO’ = 3cm. Qua A kẻ một đường thẳng cắt các đường tròn (O) và (O’) theo thứ tự tại E và F ( A nằm giữa E và F). Tính xem đoạn thẳng EF có độ dài lớn nhất bằng bao nhiêu?

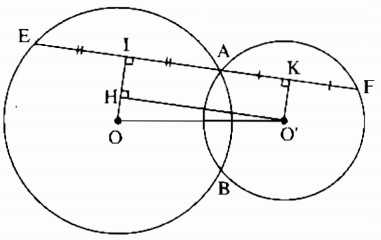
Kẻ OI ⊥ AE, O’K ⊥ AF
Trong đường tròn (O), ta có:
\( IA = IE = {1 \over 2}AE\) ( đường kính vuông góc với dây cung)
Trong đường tròn (O’), ta có:
\(KA = KF = {1 \over 2}AF\) (đường kính vuông góc với dây cung)
Ta có: EF = AE = AF
Advertisements (Quảng cáo)
Suy ra: EF = 2IA = 2AK = 2(IA + AK) = 2IK (1)
Kẻ O’H ⊥ OI
Khi đó tứ giác IHO’K là hình chữ nhật ( có ba góc vuông)
Suy ra: O’H = IK
Trong tam giác OHO’ ta có: \(O’H \le {\rm{OO’}}\) =3 (cm)
Suy ra: \(IK \le {\rm{OO}}’\) (2)
Từ (1) và (2) suy ra: \(EF \le {\rm{2OO’}}= 6 (cm)\)
Ta có: EF = 6cm khi H và O trùng nhau hay EF // OO’
Vậy EF có độ dài lớn nhất bằng 6cm khi và chỉ khi EF // OO’.
