Cho tam giác ABC vuông tại A ( AB < AC) nội tiếp đường tròn (O) có đường kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F. Chứng minh rằng:
a) Tam giác EBF là tam giác cân ;
b) Tam giác HAF là tam giác cân ;
c) HA là tiếp tuyến của đường tròn (O).

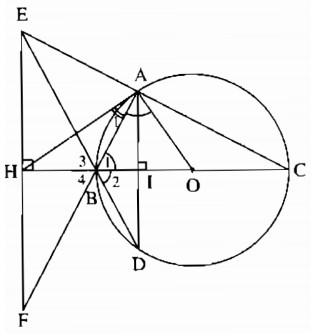
a) Gọi I là giao điểm của AD và BC
Vì BC là đường trung trực của AD nên theo tính chất đường trung trực ta có:
BA = BD
Tam giác BAD cân tại B có BI ⊥ AD nên BI là tia phân giác của góc ABD.
Suy ra: \(\widehat {ABI} = \widehat {DBI}\)
Mà \(\widehat {ABI} = \widehat {HBF}\) (đối đỉnh)
và \(\widehat {DBI} = \widehat {HBE}\) ( đối đỉnh)
Suy ra: \(\widehat {HBE} = \widehat {HBF}\)
Advertisements (Quảng cáo)
Tam giác EBF có BH là tia phân giác của góc EBF và BH ⊥ EF nên tam giác EBF cân tại B.
b) Tam giác EBF cân tại B nên HE = HF
Tam giác AEF vuông tại A có AH là đường trung tuyến ứng với cạnh huyền nên:
\(HA = HE = HF = {1 \over 2}{\rm{EF}}\) (tính chất tam giác vuông)
Vậy tam giác AHF cân tại H.
c) Tam giác AHF cân tại H nên \(\widehat {HAF} = \widehat {HFA}\) (1)
Tam giác AOB cân tại O nên \(\widehat {OAB} = \widehat {OBA}\)
Mà \(\widehat {ABI} = \widehat {HBF}\) ( đối đỉnh)
Suy ra: \(\widehat {OAB} = \widehat {HBF}\) (2)
Từ (1) và (2) suy ra: \(\widehat {HAO} = \widehat {{\rm{HAF}}} + \widehat {OAB} = \widehat {HFB} + \widehat {HBF}\) (3)
Tam giác BHF vuông tại H nên \(\widehat {HFB} + \widehat {HBF} = 90^\circ \) (4)
Từ (3) và (4) suy ra: \(\widehat {HAO} = 90^\circ \) hay HA ⊥ AO
Vậy HA là tiếp tuyến của đường tròn (O).
