Áp dụng định lý: Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền và bán kính bằng nửa cạnh huyền của tam giác vuông đó. Trả lời bài tập 2 trang 74 SGK Toán 9 tập 2 - Cánh diều - Bài 1. Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác. Tính bán kính đường tròn ngoại tiếp tam giác ABC vuông tại A với AB = 5cm, AC = 12cm...

Tính bán kính đường tròn ngoại tiếp tam giác ABC vuông tại A với AB = 5cm, AC = 12cm.

Áp dụng định lý: Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền và bán kính bằng nửa cạnh huyền của tam giác vuông đó.

Advertisements (Quảng cáo)
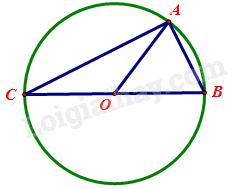
Gọi (O) là đường tròn ngoại tiếp tam giác ABC.
Xét tam giác ABC vuông tại A có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2}(Pytago)\\B{C^2} = {5^2} + {12^2}\\B{C^2} = 169\\BC = 13cm\end{array}\)
Vì ABC vuông tại A nên tâm O của đường tròn ngoại tiếp là trung điểm của cạnh huyền BC (định lý)
Vậy bán kính \(OB = OC = \frac{{BC}}{2} = \frac{{13}}{2}cm.\)
