
Trên mặt phẳng tọa độ Oxy, đường parabol ở Hình 10 biểu diễn đồ thị của hàm số \(y = a{x^2}\).
a) Tìm hệ số a.
b) Tìm điểm thuộc đồ thị hàm số có hoành độ bằng 3.
c) Tìm điểm thuộc đồ thị hàm số có tung độ bằng 4.
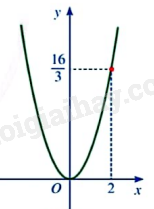

a) Thay tọa độ điểm \(\left( {2;\frac{{16}}{3}} \right)\) vào \(y = a{x^2}\) để tìm a.
b) Điểm thuộc đồ thị hàm số có hoành độ bằng 3 nên \(x = 3.\)
c) Điểm thuộc đồ thị hàm số có tung độ bằng 4 nên \(y = 4.\)

Advertisements (Quảng cáo)
a) Vì điểm \(\left( {2;\frac{{16}}{3}} \right)\) thuộc đồ thị hàm số, nên thay \(x = 2;y = \frac{{16}}{3}\) vào \(y = a{x^2}\), ta được:
\(\begin{array}{l}\frac{{16}}{3} = a{.2^2}\\a = \frac{4}{3}\end{array}\)
Vậy \(a = \frac{4}{3}\)
b) Với \(a = \frac{4}{3}\) hàm số trở thành \(y = \frac{4}{3}{x^2}.\)
Điểm thuộc đồ thị hàm số có hoành độ bằng 3 nên \(x = 3,\) ta có:
\(\begin{array}{l}y = \frac{4}{3}{x^2}\\y = \frac{4}{3}{.3^2} = 12.\end{array}\)
Vậy điểm cần tìm là \(\left( {3;12} \right)\).
c) Điểm thuộc đồ thị hàm số có tung độ bằng 4 nên \(y = 4.\) Ta có:
\(\begin{array}{l}y = \frac{4}{3}{x^2}\\4 = \frac{4}{3}{x^2}\end{array}\)
\(x = \pm \sqrt 3 \)
Vậy điểm cần tìm là \(\left( {\sqrt 3 ;4} \right),\left( { - \sqrt 3 ;4} \right).\)
