Hoạt động1
Trả lời câu hỏi Hoạt động 1 trang 82
Cho tam giác \(ABC\) vuông tại \(A\) (Hình 13).
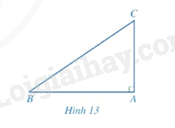
a) Biểu diễn \(\sin B,\cos C\) theo \(AC,BC\).
b) Viết công thức tính \(AC\) theo \(BC\) và \(\sin B\).
c) Viết công thức tính \(AC\) theo \(BC\) và \(\cos C\).
Dựa vào định nghĩa tỉ số lượng giác để giải bài toán.
a) \(\sin B = \frac{{AC}}{{BC}}\);\(\cos C = \frac{{AC}}{{BC}}\).
b) \(AC = BC.\sin B\).
c) \(AC = BC.\cos C\).
Luyện tập1
Trả lời câu hỏi Luyện tập 1 trang 83
Tính độ cao \(AC\) trong Hình 12b khi \(BC = 20m\) (làm tròn kết quả đến hàng phần mười của mét)
Dựa vào quan hệ giữa cạnh huyền và tỉ số lượng giác của góc nhọn để tính.
Độ cao AC là:
\(AC = BC.\cos 25^\circ = 20.\cos 25^\circ \approx 18,1\left( m \right)\).
Luyện tập2
Trả lời câu hỏi Luyện tập 2 trang 83
Cho tam giác nhọn \(ABC\) có đường cao \(CK\). Biểu thị \(CK\) theo \(AC\) và \(\sin A\). Từ đó, chứng minh diện tích tam giác \(ABC\) bằng \(\frac{1}{2}.AB.AC.\sin A\).
Dựa vào định nghĩ tỉ số lượng giác kết hợp với mối quan hệ giữa cạnh góc vuông, cạnh huyền và tỉ số lượng giác để giải bài toán.
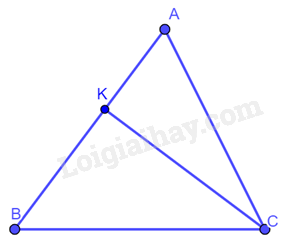
Vì tam giác \(ACK\) vuông tại \(K\) nên: \(CK = AC.\sin A\).
Ta có: \({S_{ABC}} = \frac{1}{2}CK.AB = \frac{1}{2}.AB.AC.\sin A\).