Hoạt động2
Trả lời câu hỏi Hoạt động 2 trang 84
Cho tam giác \(ABC\) vuông tại \(A\) (Hình 17)
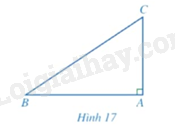
a) Biểu diễn \(\tan B,\cot C\) theo \(AB,AC\).
b) Viết công thức tính \(AC\) theo \(AB\) và \(\tan B\).
c) Viết công thức tính \(AC\) theo \(AB\) và \(\cot C\).

Dựa vào định nghĩa tỉ số lượng giác để giải bài toán.

a) Vì tam giác \(ABC\) vuông tại \(A\) nên:
\(\tan B = \frac{{CA}}{{AB}}\);\(\cot C = \frac{{AC}}{{AB}}\).
Advertisements (Quảng cáo)
b) Ta có: \(AC = AB.\tan B\).
c) Ta có: \(AC = AB.\cot C\).
Luyện tập3
Trả lời câu hỏi Luyện tập 3 trang 84
Tính \(AB\) trong Hình 17 khi \(AC = 4cm\) và \(\widehat B = 34^\circ \) (làm tròn kết quả đến hàng phần mười của centimét).
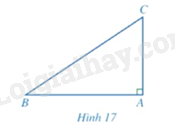

Dựa vào mỗi quan hệ giữa cạnh góc vuông và tỉ số lượng giác để giải bài toán.

Vì tam giác \(ABC\) vuông tại \(A\) nên:
\(AC = AB.\tan B = 4.\tan 34^\circ \approx 2,7\left( {cm} \right)\).
