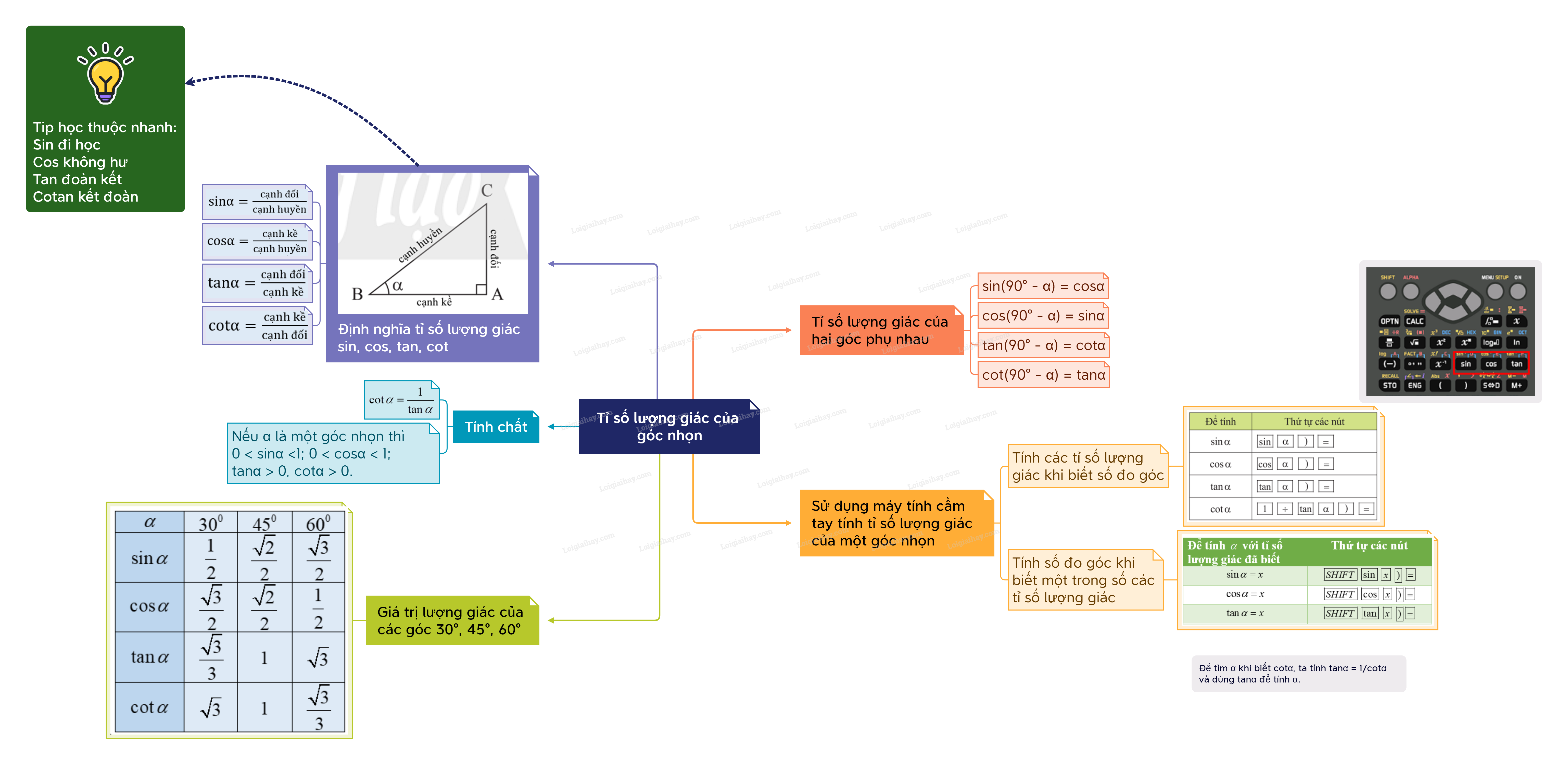
1. Định nghĩa tỉ số lượng giác của một góc nhọn
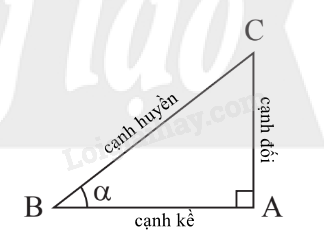
|
\({\rm{sin\alpha }} = \frac{{cạnh\,đối}}{{cạnh\,huyền}};{\rm{cos\alpha }} = \frac{{cạnh\,kề}}{{cạnh\,huyền}};\) \({\rm{tan\alpha }} = \frac{{cạnh\,đối}}{{cạnh\,kề}};{\rm{cot\alpha }} = \frac{{cạnh\,kề}}{{cạnh\,đối}}.\) \(\cot \alpha = \frac{1}{{\tan \alpha }}\).
|
Tip học thuộc nhanh:
|
Sin đi học Cos không hư Tan đoàn kết Cotan kết đoàn |
Chú ý: Với góc nhọn \(\alpha \), ta có:
\(0
\(\cot \alpha = \frac{1}{{\tan \alpha }}\).
Ví dụ:
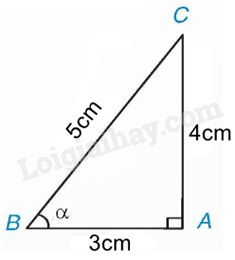
Theo định nghĩa của tỉ số lượng giác, ta có:
\(\sin \alpha = \frac{{AC}}{{BC}} = \frac{4}{5}\), \(\cos \alpha = \frac{{AB}}{{BC}} = \frac{3}{5}\), \(\tan \alpha = \frac{{AC}}{{AB}} = \frac{4}{3}\), \(\cot \alpha = \frac{{AB}}{{AC}} = \frac{3}{4}\)
Bảng giá trị lượng giác của các góc nhọn đặc biệt
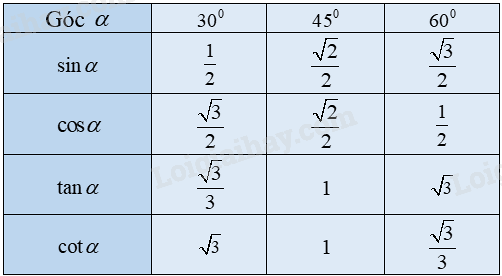
Ví dụ: \(P = \frac{{\sin {{30}^0}.\cos {{60}^0}}}{{\tan {{45}^0}}} = \frac{{\frac{1}{2}.\frac{1}{2}}}{1} = \frac{1}{4}\).
2. Tỉ số lượng giác của hai góc phụ nhau
Định lý về tỉ số lượng giác của hai góc phụ nhau
|
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tan góc này bằng côtang góc kia. \(\begin{array}{*{20}{c}}{\sin \left( {{{90}^0} - \alpha } \right) = \cos \alpha ;}&{\cos \left( {{{90}^0} - \alpha } \right) = \sin \alpha ;}\\{\tan \left( {{{90}^0} - \alpha } \right) = \cot \alpha ;}&{\cot \left( {{{90}^0} - \alpha } \right) = \tan \alpha .}\end{array}\) |
Ví dụ:
Advertisements (Quảng cáo)
\(\begin{array}{l}\sin {60^0} = \cos \left( {{{90}^0} - {{60}^0}} \right) = \cos {30^0};\\\cos {52^0}30′ = \sin \left( {{{90}^0} - {{52}^0}30′} \right) = \sin {37^0}30′;\\\tan {80^0} = \cot \left( {{{90}^0} - {{80}^0}} \right) = \cot {10^0};\\\cot {82^0} = \tan \left( {{{90}^0} - {{82}^0}} \right) = \tan {8^0}.\end{array}\)
3. Sử dụng máy tính cầm tay tính tỉ số lượng giác của một góc nhọn
Người ta thường dùng các đơn vị số đo góc là độ (kí hiệu: \(^0\)), phút (kí hiệu: \(‘\)), giây (kí hiệu: \(”\)).
Ta có thể sử dụng nhiều loại máy tính cầm tay để tính các tỉ số lượng giác của góc nhọn và tính số đo của góc nhọn khi biết một tỉ số lượng giác của nó.
Lưu ý: ta cần đổi đơn vị đo về độ.

Tính các tỉ số lượng giác của các góc nhọn
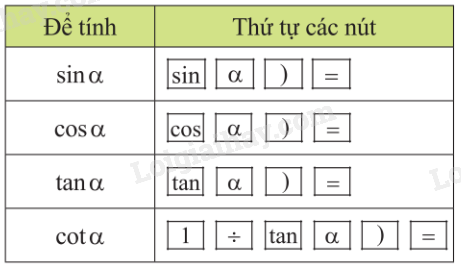
Để tính tỉ số lượng giác của một góc \(\alpha \), ta dùng các nút:

Để tính \(\cot \alpha \), ta tính \(\cot \alpha = \frac{1}{{\tan \alpha }}\) hoặc \(\tan \left( {{{90}^0} - \alpha } \right)\).
Bảng tóm tắt cách tính tỉ số lượng giác của một góc nhọn
Xác định số đo của góc nhọn khi biết một tỉ số lượng giác của góc đó
Bảng tóm tắt cách tính số đo của một góc nhọn khi biết một tỉ số lượng giác
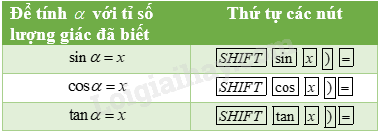
Để tìm \(\alpha \) khi biết \(\cot \alpha \), ta tính \(\tan \alpha = \frac{1}{{\cot \alpha }}\) và dùng \(\tan \alpha \) để tính \(\alpha \).
Một số công thức mở rộng:
+) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
+) \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\)
+) \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\)
+) \(\tan \alpha .\cot \alpha = 1\)
+) \(\frac{1}{{{{\cos }^2}\alpha }} = {\tan ^2}\alpha + 1\)
+) \(\frac{1}{{{{\sin }^2}\alpha }} = {\cot ^2}\alpha + 1\)