Hoạt động2
Trả lời câu hỏi Hoạt động 2 trang 47
a) Thực hiện các phép tính cho trên bảng trong Hình 1.
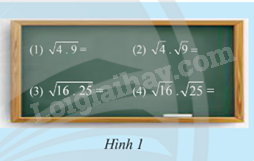
b) Từ đó, có nhận xét gì về căn bậc hai của tích hai số không âm?

Dựa vào \({\left( {\sqrt a } \right)^2} = {\left( { - \sqrt a } \right)^2} = a\) và \(\sqrt {{a^2}} = a\). ( a > 0)

a)
(1) \(\sqrt {4.9} = \sqrt {36} = \sqrt {{{\left( 6 \right)}^2}} = 6\)
(2) \(\sqrt 4 .\sqrt 9 = \sqrt {{2^2}} .\sqrt {{3^2}} = 2.3 = 6\)
(3) \(\sqrt {16.25} = \sqrt {400} = \sqrt {{{\left( {20} \right)}^2}} = 20\)
(4) \(\sqrt {16} .\sqrt {25} = \sqrt {{4^2}} .\sqrt {{5^2}} = 4.5 = 20\)
b) Căn bậc hai của tích hai số không âm bằng tích các căn bậc hai của hai số không âm.
Hoạt động3
Trả lời câu hỏi Hoạt động 3 trang 48
Thay mỗi ? bằng các số thích hợp:
a) \(\sqrt {50} = \sqrt ? .\sqrt 2 = ?.\sqrt 2 \)
b) \(\sqrt {3.{{( - 4)}^2}} = \sqrt ? .\sqrt 3 = ?.\sqrt 3 \)
c) \(3\sqrt 2 = \sqrt ? .\sqrt 2 = \sqrt ? \)
d) \( - 2\sqrt 5 = - \sqrt ? .\sqrt 5 = - \sqrt ? \)

Dựa vào tính chất \(\sqrt {a.b} = \sqrt a .\sqrt b \) với a, b > 0

a) \(\sqrt {50} = \sqrt {25} .\sqrt 2 = 5.\sqrt 2 \)
b) \(\sqrt {3.{{( - 4)}^2}} = \sqrt {16} .\sqrt 3 = 4.\sqrt 3 \)
c) \(3\sqrt 2 = \sqrt 9 .\sqrt 2 = \sqrt {18} \)
Thực hành3
Trả lời câu hỏi Thực hành 3 trang 49
Tính
a) \(\sqrt {0,16.64} \)
b) \(\sqrt {8,{{1.10}^3}} \)
c) \(\sqrt {12.250.1,2} \)
d) \(\sqrt {28} .\sqrt 7 \)
e) \(\sqrt {4,9} .\sqrt {30} .\sqrt {12} \)

Dựa vào tính chất \(\sqrt {a.b} = \sqrt a .\sqrt b \) với a, b > 0

a) \(\sqrt {0,16.64} = \sqrt {0,16} .\sqrt {64} = 0,4.8 = 3,2\)
b) \(\sqrt {8,{{1.10}^3}} = \sqrt {81} .\sqrt {{{10}^2}} = 9.10 = 90\)
c) \(\sqrt {12.250.1,2} = \sqrt {12.25.10.1,2} = \sqrt {12.25.12} \)
Advertisements (Quảng cáo)
\( = \sqrt {12.25.12} = \sqrt {{{25.12}^2}} = \sqrt {25} .\sqrt {{{12}^2}} = 5.12 = 60\)
d) \(\sqrt {28} .\sqrt 7 = \sqrt {28.7} = \sqrt {196} = \sqrt {{{14}^2}} = 14\)
e) \(\sqrt {4,9} .\sqrt {30} .\sqrt {12} = \sqrt {4,9.30.12} = \sqrt {1764} = \sqrt {{{42}^2}} = 42\)
Thực hành4
Trả lời câu hỏi Thực hành 4 trang 49
Rút gọn các biểu thức sau:
a) \(\sqrt {500} \)
b) \(\sqrt {5a} .\sqrt {20a} \) với a \( \ge \)0
c) \(\sqrt {18.{{\left( {2 - a} \right)}^2}} \) với a > 2

Dựa vào tính chất \(\sqrt {a.b} = \sqrt a .\sqrt b \) với a, b > 0

a) \(\sqrt {500} = \sqrt {5.100} = \sqrt 5 .\sqrt {100} = 10\sqrt 5 \)
b) \(\sqrt {5a} .\sqrt {20a} = \sqrt {5a.20a} = \sqrt {100{a^2}} = \sqrt {100} .\sqrt {{a^2}} = 10a\)
c) \(\sqrt {18.{{\left( {2 - a} \right)}^2}} = \sqrt {9.2.{{\left( {2 - a} \right)}^2}} \)\( = \sqrt 9 .\sqrt 2 .\sqrt {{{\left( {2 - a} \right)}^2}} \)\( = 3\sqrt 2 .\left| {2 - a} \right| = 3\sqrt 2 (a - 2)\)
Thực hành5
Trả lời câu hỏi Thực hành 5 trang 49
Đưa thừa số vào trong dấu căn bậc hai:
a) \(5.\sqrt 2 \)
b) \( - 10\sqrt 7 \)
c) \(2a\sqrt {\frac{3}{{10a}}} \) với a > 0

Dựa vào tính chất \(\sqrt {a.b} = \sqrt a .\sqrt b \) với a, b > 0

a) \(5.\sqrt 2 = \sqrt {{5^2}.2} = \sqrt {50} \)
b) \( - 10\sqrt 7 = - \sqrt {{{10}^2}.7} = - \sqrt {700} \)
c) \(\sqrt {{{\left( {2a} \right)}^2}.\frac{3}{{10a}}} = \sqrt {\frac{{12{a^2}}}{{10a}}} = \sqrt {\frac{{6a}}{5}} \).
Vận dụng1
Trả lời câu hỏi Vận dụng 1 trang 49
Tính diện tích của hình chữ nhật và hình vuông trong hoạt động khởi động. Biết mỗi ô vuông nhỏ có độ dài cạnh là 1. Diện tích của hai hình đó bằng nhau không?
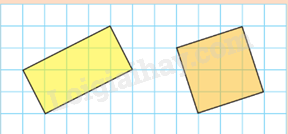

Dựa vào công thức tính diện tích hình chữ nhật và hình vuông.

Độ dài chiều dài hình chữ nhật là: \(\sqrt {{4^2} + {2^2}} = 2\sqrt 5 \)
Độ dài chiều rộng hình chữ nhật là: \(\sqrt {{2^2} + {1^2}} = \sqrt 5 \)
Diện tích hình chữ nhật là: \(2\sqrt 5 .\sqrt 5 = 2.5 = 10\)
Độ dài cạnh hình vuông là: \(\sqrt {{3^2} + {1^2}} = \sqrt {10} \)
Diện tích hình vuông là: \({\left( {\sqrt {10} } \right)^2} = 10\)
Vậy diện tích hai hình bằng nhau.
