Hoạt động2
Trả lời câu hỏi Hoạt động 2 trang 54
Hình vuông ABCD được chia thành hai hình vuông và hai hình chữ nhật như Hình 3.
a) Tính độ dài đường chéo của hai hình vuông AMIN và CEIF.
b) Tính độ dài đường chéo của hai hình vuông ABCD theo hai cách khác nhau.
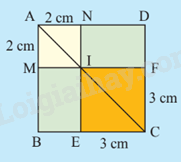

- Tính độ dài đường chéo AMIN bằng cách dựa vào định lý Pythagore vào tam giác vuông AMI và tính độ dài đường chéo EIFC bằng cách dựa vào định lý Pythagore vào tam giác vuông IFC.- C1: Từ phần a suy ra độ dài đường chéo ABCD = độ dài đường chéo AMNI + độ dài đường chéo IFCE.- C2: Tính độ dài cạnh AB và BC suy ra đường chéo hình vuông ABCD bằng cách áp dụng định lý Pythagore vào tam giác vuông ABC.

a)Xét tam giác vuông AMI có AI = \(\sqrt {{2^2} + {2^2}} = 2\sqrt 2 \)cm
Vậy độ dài đường chéo AMIN bằng \(2\sqrt 2 \) cm
Xét tam giác vuông IFC có IC = \(\sqrt {{3^2} + {3^2}} = 3\sqrt 2 \)cm
Vậy độ dài đường chéo AMIN bằng \(3\sqrt 2 \) cm.
b) Cách 1:
Ta có: độ dài đường chéo ABCD = độ dài đường chéo AMNI + độ dài đường chéo IFCE = \(2\sqrt 2 \) + \(3\sqrt 2 \) = \(5\sqrt 2 \) cm.
Cách 2:
Độ dài cạnh AB là : 2 + 3 = 5 cm
Độ dài cạnh BC là : 2 + 3 = 5 cm
Xét tam giác vuông ABC có: AC = \(\sqrt {A{B^2} + B{C^2}} = \sqrt {{5^2} + {5^2}} = 5\sqrt 2 \) cm.
Vậy độ dài đường chéo của hình vuông ABCD là \(5\sqrt 2 \) cm.
Thực hành3
Trả lời câu hỏi Thực hành 3 trang 55
Rút gọn các biểu thức sau:
a) \(\sqrt {20} - \sqrt 5 \)
b) \(\sqrt {32} - \sqrt {18} + \frac{4}{{\sqrt 2 }}\)
c) \(\left( {2 - \sqrt {10} } \right)\left( {2 - \sqrt 5 } \right)\)

Dựa vào VD5 trang 55 làm tương tự.

a) \(\sqrt {20} - \sqrt 5 = \sqrt {{2^2}.5} - \sqrt 5 = 2\sqrt 5 - \sqrt 5 = \sqrt 5 \)
Advertisements (Quảng cáo)
b)\(\sqrt {32} - \sqrt {18} + \frac{4}{{\sqrt 2 }}\)\( = \sqrt {16.2} - \sqrt {9.2} + \frac{4}{{\sqrt 2 }}\)\( = 4\sqrt 2 - 3\sqrt 2 + \frac{4}{{\sqrt 2 }}\)\( = \sqrt 2 + \frac{4}{{\sqrt 2 }}\)\( = \sqrt 2 .\sqrt 2 + 4\)\( = 2 + 4 = 6\)
c) \(\left( {2 - \sqrt {10} } \right)\left( {2 - \sqrt 5 } \right)\)\( = 4 - 2\sqrt 5 - 2\sqrt {10} + \sqrt {10} .\sqrt 5 \)\( = 4 - 2\sqrt 5 + \left( {\sqrt 5 - 2} \right)\sqrt {10} \)
Thực hành4
Trả lời câu hỏi Thực hành 4 trang 56
Rút gọn các biểu thức sau:
a) \(\frac{2}{3}\sqrt {9{x^3}} + 4x\sqrt {\frac{x}{4}} - {x^2}\sqrt {\frac{1}{x}} \) với x > 0
b) \(\frac{{{a^2} - 5}}{{a + \sqrt {15} }}\) với a \( \ne - \sqrt 5 \)

Dựa vào VD6 trang 55 làm tương tự.

a) \(\frac{2}{3}\sqrt {9{x^3}} + 4x\sqrt {\frac{x}{4}} - {x^2}\sqrt {\frac{1}{x}} \)
\(\begin{array}{l} = \frac{2}{3}.3\sqrt {{x^2}.x} + 4x.\frac{1}{2}\sqrt x - \sqrt {{x^4}\frac{1}{x}} \\ = 2x\sqrt x + 2x\sqrt x - \sqrt {{x^3}} \\ = 4x\sqrt x - x\sqrt x \\ = 3x\sqrt x \end{array}\)
b) \(\frac{{{a^2} - 5}}{{a + \sqrt 5 }}\) với a \( \ne - \sqrt 5 \)
\(\frac{{{a^2} - 5}}{{a + \sqrt 5 }} = \frac{{\left( {a + \sqrt 5 } \right)\left( {a - \sqrt 5 } \right)}}{{a + \sqrt 5 }} = a - \sqrt 5 \)
Vận dụng2
Trả lời câu hỏi Vận dụng 2 trang 56
Trả lời câu hỏi trong hoạt động khởi động trang 52.
Một khu đất hình tam giác vuông tiếp giáp với hai thửa ruộng hình vuông có diện tích như hình bên. Khu đất hình tam giác vuông có chu vi bằng chu vi thửa ruộng bé không? Kiểm tra bằng cách nào?
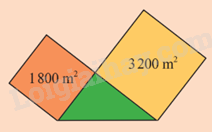

- Tính cạnh thửa ruộng bé hình vuông và cạnh thửa ruộng lớn hình vuông.
- Tính cạnh còn lại của tam giác vuông bằng cách áp dụng định lý pythagore khi biết 2 cạnh của 2 hình vuông.
- Tính chu vi hình vuông bé và chu vi tam giác vuông và so sánh.

Cạnh thửa ruộng bé hình vuông là: \(\sqrt {1800} = 30\sqrt 2 \)m.
Chu vi thửa ruộng bé là: \(30\sqrt 2 .4 = 120\sqrt 2 \)m
Cạnh thửa ruộng lớn hình vuông là: \(\sqrt {3200} = 40\sqrt 2 \) m
Cạnh của tam giác vuông là: \(\sqrt {{{(30\sqrt 2 )}^2} + {{(40\sqrt 2 )}^2}} = 50\sqrt 2 \) m
Chu vi tam giác vuông là: \(30\sqrt 2 + 40\sqrt 2 + 50\sqrt 2 = 120\sqrt 2 \) m.
Vậy khu đất hình tam giác vuông có chu vi bằng chu vi thửa ruộng bé.
