
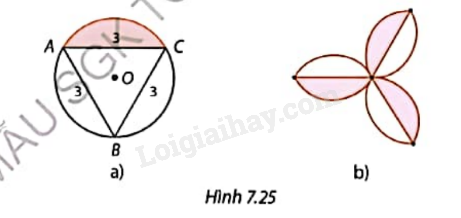
Bạn An sử dụng các hình viên phân như Hình 7.25a để ghép thành mẫu hoa văn trang trí như trong Hình 7.25b. Tính diện tích của mẫu hoa văn.

Tính bán kính đường tròn ngoại tiếp của tam giác đều bằng \(\frac{{a\sqrt 3 }}{3}\).
Tính diện tích đường tròn nội tiếp của tam giác đều là S = \(\pi {R^2}\)
Tính diện tích tam giác đều \(\frac{{{a^2}\sqrt 3 }}{4}\) với cạnh a rồi lấy diện tích đường tròn trừ đi diện tích tam giác ta tìm được diện tích một viên phân.

Advertisements (Quảng cáo)
Ta có bán kính đường tròn ngoại tiếp của tam giác đều bằng \(\sqrt 3 \).
Diện tích đường tròn nội tiếp của tam giác đều là:
S = \(\pi {\left( {\sqrt 3 } \right)^2} = 3\pi \) cm2
Diện tích tam giác đều ABC là: \(\frac{{9\sqrt 3 }}{4}\) cm2
Diện tích 3 viên phân là:
\(3\pi - \frac{{9\sqrt 3 }}{4} \approx 5,5\) cm2
Mà mẫu hoa văn tạo thành từ 6 viên phân nên có diện tích là:
2.5,5 \( \approx \) 11 cm2.
