Tính bán kính đường tròn ngoại tiếp hình vuông bằng nửa đường chéo. Suy ra bán kính ngoại tiếp hình chữ nhật. Lời giải bài tập, câu hỏi bài tập 7.22 trang 40 SGK Toán 9 tập 2 - Cùng khám phá - Ôn tập chương 7. Hình vuông ABCD có cạnh 4 cm và hình chữ nhật MNPQ có chiều rộng 2 cm cùng nội tiếp trong đường tròn (O) (Hình 7. 26). Tính chiều dài MQ của hình chữ nhật...
Hình vuông ABCD có cạnh 4 cm và hình chữ nhật MNPQ có chiều rộng 2 cm cùng nội tiếp trong đường tròn (O) (Hình 7.26). Tính chiều dài MQ của hình chữ nhật.
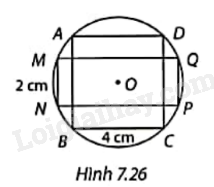
Tính bán kính đường tròn ngoại tiếp hình vuông bằng nửa đường chéo. Suy ra bán kính ngoại tiếp hình chữ nhật, sau đó tính đường chéo hình chữ nhật để suy ra chiều dài hình chữ nhật.
Advertisements (Quảng cáo)
Đường chéo hình vuông là: \(\sqrt {{4^2} + {4^2}} = 4\sqrt 2 \)cm Bán kính đường tròn ngoại tiếp hình vuông OA bằng nửa đường chéo là: \(2\sqrt 2 \)cm
Suy ra OM = OA = \(2\sqrt 2 \) cm, nên ta có:
MP = 2. OM = \(4\sqrt 2 \) cm.
Xét tam giác vuông MQP vuông tại Q, ta có:
MQ = \(\sqrt {M{P^2} - Q{P^2}} = \sqrt {{{\left( {4\sqrt 2 } \right)}^2} - {2^2}} = 2\sqrt 7 \) cm.