Hoạt động2
Đáp án câu hỏi Hoạt động 2 trang 32
Trong Hình 7.6, O là giao điểm của ba đường phân giác của \(\Delta \)ABC và OM, ON, OP là các đường vuông góc hạ từ O xuống ba cạnh của tam giác. Giải thích vì sao đường tròn tâm O bán kính OM tiếp xúc cả ba cạnh của \(\Delta \)ABC.
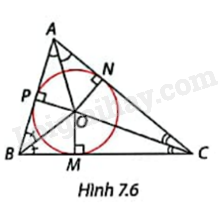

Ba đường phân giác của một tam giác cùng đi qua một điểm và điểm này cách đều ba cạnh của tam giác.

Ta có ba đường phân giác của tam giác ABC cùng đi qua một điểm O nên ta có OP = ON = OM. Vì vậy đường tròn tâm O bán kính OM tiếp xúc cả ba cạnh của \(\Delta \)ABC.
Luyện tập2
Gợi ý giải câu hỏi Luyện tập 2 trang 33
Tính bán kính đường tròn nội tiếp tam giác đều ABC có cạnh là \(2\sqrt 3 \)cm.

Đường tròn nội tiếp của tam giác đều cạnh a có tâm là trọng tâm tam giác đều và bán kính bằng \(\frac{{a\sqrt 3 }}{6}\).

Bán kính đường tròn nội tiếp tam giác đều ABC có cạnh là \(2\sqrt 3 \)cm là \(\frac{{2\sqrt 3 .\sqrt 3 }}{6} = 1\) cm.
Vận dụng
Gợi ý giải câu hỏi Vận dụng trang 33
Advertisements (Quảng cáo)
Tam giác đều ABC có cạnh bằng 6 cm. Tính tổng chu vi của \(\Delta \)ABC, chu vi đường tròn nội tiếp và chu vi đường tròn ngoại tiếp của nó. Từ đó trả lời câu hỏi của bài toán ở phần Khởi động.
Phần Khởi động: Bạn Uyên dùng một sợi thép để uốn thành mẫu hoạ tiết (Hình 7.1). Độ dài của sợi thép ít nhất là bao nhiêu để tam giác đều trong mẫu hoạ tiết có cạnh bằng 6 cm?


Chu vi tam giác đều P = 3a
Bán kính đường tròn nội tiếp của tam giác đều bằng \(\frac{{a\sqrt 3 }}{6}\).
Chu vi đường tròn nội tiếp của tam giác đều là S = \(2\pi r\)
Bán kính đường tròn ngoại tiếp của tam giác đều bằng \(\frac{{a\sqrt 3 }}{3}\).
Chu vi đường tròn ngoại tiếp của tam giác đều là S = \(2\pi R\)

Chu vi tam giác đều P = 3a = 3.6 = 18 cm.
Bán kính đường tròn nội tiếp của tam giác đều bằng \(\frac{{a\sqrt 3 }}{6} = \frac{{6\sqrt 3 }}{6} = \sqrt 3 \)cm.
Chu vi đường tròn nội tiếp của tam giác đều là S = \(2\pi r = 2\sqrt 3 \pi \).
Bán kính đường tròn ngoại tiếp của tam giác đều bằng \(\frac{{a\sqrt 3 }}{3} = \frac{{6\sqrt 3 }}{3} = 2\sqrt 3 \)cm.
Chu vi đường tròn ngoại tiếp của tam giác đều là S = \(2\pi R = 4\sqrt 3 \pi \)cm.
Vậy độ dài của sợi thép ít nhất là: \(18 + 2\sqrt 3 \pi + 4\sqrt 3 \pi \approx 50,65\)cm.
