Câu hỏi/bài tập:

Cho tam giác đều ABC có cạnh bằng 3cm và nội tiếp đường tròn (O) như Hình 9.26.
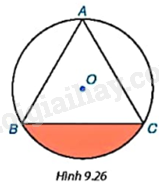
a) Tính bán kính R của đường tròn (O).
b) Tính diện tích hình viên phân giới hạn bởi dây cung BC và cung nhỏ BC.

a) + Vẽ đường cao AH của tam giác ABC, nên AH đồng thời là đường trung trực, đường trung tuyến của tam giác.
+ Chứng minh O vừa là giao điểm ba đường trung trực vừa là trọng tâm.
+ Chứng minh được \(OA = \frac{2}{3}AH\).
+ Áp dụng định lý Pythagore tam giác AHB vuông tại H để tính AH. Từ đó tính được OA.
b) + Tính \({S_1}\) là diện tích hình quạt tròn BOC, tính diện tích tam giác BOC.
+ Khi đó, Sviên phân \( = {S_1} - {S_{BOC}}\).

Advertisements (Quảng cáo)
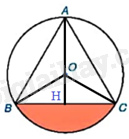
Vẽ đường cao AH của tam giác ABC. Tam giác ABC đều nên AH vừa là đường cao, vừa là đường trung tuyến, vừa là đường trung trực của tam giác ABC.
Vì \(\Delta \)ABC đều nên tâm O của đường tròn ngoại tiếp \(\Delta \)ABC đồng thời là trọng tâm của tam giác.
Ta có: \(BH = \frac{{BC}}{2} = \frac{3}{2}cm\)
Xét tam giác AHB vuông tại H, theo định lý Pythagore ta có:
\(A{H^2} + B{H^2} = A{B^2} \Rightarrow AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{3^2} - {{\left( {\frac{3}{2}} \right)}^2}} = \frac{{3\sqrt 3 }}{2}\left( {cm} \right)\)
Vì O là trọng tâm của \(\Delta \)ABC, AH là đường trung tuyến của \(\Delta \)ABC nên
\(OA = \frac{2}{3}AH = \frac{2}{3}.\frac{{3\sqrt 3 }}{2} = \sqrt 3 \left( {cm} \right)\)
b) Ta có: \(OH = AH - OA = \frac{{3\sqrt 3 }}{2} - \sqrt 3 = \frac{{\sqrt 3 }}{2}\left( {cm} \right)\)
Ta có: sđ$\overset\frown{BC}=2\widehat{BAC}={{120}^{o}}$ (góc nội tiếp chắn cung nhỏ BC của đường tròn (O))
Diện tích hình quạt tròn BOC là:
\({S_1} = \frac{{120}}{{360}}.\pi .{\left( {\sqrt 3 } \right)^2} = \pi \left( {c{m^2}} \right)\)
Diện tích tam giác BOC là:
\({S_{BOC}} = \frac{1}{2}OH.BC = \frac{1}{2}.\frac{{\sqrt 3 }}{2}.3 = \frac{{3\sqrt 3 }}{4}\left( {c{m^2}} \right)\)
Diện tích hình viên phân giới hạn bởi dây cung BC và cung nhỏ BC là:
Sviên phân \( = {S_1} - {S_{BOC}} = \pi - \frac{{3\sqrt 3 }}{4}\left( {c{m^2}} \right)\)
