Hoạt động (HĐ) 1
Trả lời câu hỏi Hoạt động 1 trang 72 SGK Toán 9
Cho d là đường trung trực của đoạn thẳng AB và O là một điểm trên d (H.9.12). Hỏi đường tròn tâm O đi qua điểm A thì có đi qua điểm B không?
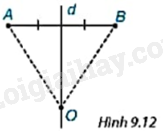

Chứng minh \(OA = OB\), suy ra đường tròn tâm O đi qua điểm A thì đi qua điểm B.

Do O thuộc đường trung trực của AB nên \(OA = OB\).
Suy ra, đường tròn tâm O đi qua điểm A thì đi qua điểm B.
Hoạt động (HĐ) 2
Trả lời câu hỏi Hoạt động 2 trang 72SGK Toán 9
Cho tam giác ABC có ba đường trung trực đồng quy tại O (H.9.13). Hãy giải thích tại sao đường tròn (O; OA) đi qua ba đỉnh của tam giác ABC.
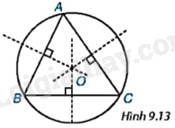

+ Dùng tính chất ba đường trung trực trong tam giác suy ra \(OA = OB = OC\).
+ Suy ra, đường tròn (O; OA) đi qua ba đỉnh của tam giác ABC.

Vì tam giác ABC có ba đường trung trực đồng quy tại O nên \(OA = OB = OC\).
Do đó, 3 điểm A, B, C thuộc đường tròn đường kính OA.
Vậy đường tròn (O; OA) đi qua ba đỉnh của tam giác ABC
Câu hỏi
Gợi ý giải câu hỏi Câu hỏi trang 73 SGK Toán 9
Hãy kể tên bốn tam giác nội tiếp đường tròn (O) trong Hình 9.14.
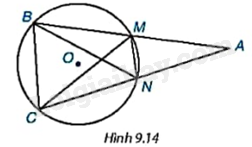

Chỉ ra 4 điểm B, C, M, N thuộc đường tròn (O) nên các tam giác MNC, MNB, BCM, BCN nội tiếp đường tròn (O).

Vì 4 điểm B, C, M, N thuộc đường tròn (O) nên các tam giác MNC, MNB, BCM, BCN nội tiếp đường tròn (O).
Hoạt động (HĐ) 3
Giải câu hỏi Hoạt động 3 trang 73 SGK Toán 9
Cho tam giác ABC vuông tại đỉnh A (H.9.15). Gọi N, P lần lượt là trung điểm của các cạnh AB và AC.
a) Vẽ hai đường trung trực a, b của các cạnh AB, AC, cắt nhau tại M.
b) Hãy giải thích vì sao MN, MP là các đường trung bình của tam giác ABC.
c) Hãy giải thích vì sao M là trung điểm của BC, từ đó suy ra đường tròn ngoại tiếp của tam giác ABC có tâm M và bán kính \(MB = MC = \frac{{BC}}{2}\).
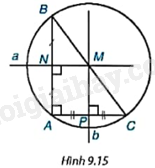

a) Vẽ đường thẳng a vuông góc với AB tại N thì a là đường trung trực của cạnh AB.
Vẽ đường thẳng b vuông góc với AC tại P thì b là đường trung trực của cạnh AC.
b) + Chứng minh a//AC, b//AB.
+ Sử dụng tính chất: Trong một tam giác, nếu một đường thẳng đi qua trung điểm một cạnh và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba chứng minh được MN, MP là các đường trung bình của tam giác ABC.
c) Chứng minh tứ giác ANMP là hình chữ nhật, suy ra \(\widehat {NMP} = {90^o}\).
Chứng minh được \(\widehat {BMN} = {180^o}\) nên 3 điểm M, B, C thẳng hàng. Mà \(MB = MC = AM\), M là trung điểm của BC. Từ đó suy ra đường tròn ngoại tiếp của tam giác ABC có tâm M và bán kính \(MB = MC = \frac{{BC}}{2}\).

a) Vẽ đường thẳng a vuông góc với AB tại N thì a là đường trung trực của cạnh AB.
Vẽ đường thẳng b vuông góc với AC tại P thì b là đường trung trực của cạnh AC.
b) Vì tam giác ABC vuông tại A nên \(AB \bot AC\), vì a là trung trực của AB nên \(a \bot AB\), suy ra: a//AC.
Vì b là đường trung trực của AC nên \(b \bot AC\), mà \(AB \bot AC\)(cmt) nên b//AB.
Xét tam giác ABC có:
+ Vì a//AC, mà N là trung điểm của AB nên đường thẳng a đi qua trung điểm của BC. Do đó, MN là đường trung bình của tam giác ABC.
+ Vì b//AB, mà P là trung điểm của AC nên đường thẳng b đi qua trung điểm của BC. Do đó, MP là đường trung bình của tam giác ABC.
c) Tứ giác ANMP có: \(\widehat {NAP} = \widehat {MPA} = \widehat {MNA} = {90^o}\) nên tứ ANMP là hình chữ nhật. Do đó, \(\widehat {NMP} = {90^o}\).
Vì M thuộc đường trung trực của AB nên \(BM = MA\). Suy ra, tam giác BAM cân tại M. Do đó, MN là đường trung trực đồng thời là đường phân giác của tam giác. Do đó, \(\widehat {BMN} = \widehat {NMA}\).
Advertisements (Quảng cáo)
Vì M thuộc đường trung trực của AC nên \(MA = MC\). Suy ra, tam giác CAM cân tại M. Do đó, MP là đường trung trực đồng thời là đường phân giác của tam giác. Do đó, \(\widehat {CMP} = \widehat {PMA}\).
Ta có: \(\widehat {BMC} = \widehat {BMN} + \widehat {NMA} + \widehat {AMP} + \widehat {PMC} = 2\left( {\widehat {NMA} + \widehat {AMP}} \right) = 2.\widehat {NMP} = {180^o}\)
Do đó, ba điểm M, B, C thẳng hàng. Suy ra, \(MA = MB = MC = \frac{{BC}}{2}\).
Suy ra, đường tròn ngoại tiếp của tam giác ABC có tâm M và bán kính \(MB = MC = \frac{{BC}}{2}\).
Luyện tập (LT) 1
Hướng dẫn giải câu hỏi Luyện tập 1 trang 73 SGK Toán 9
Cho tam giác ABC có \(AC = 3cm,AB = 4cm\) và \(BC = 5cm\). Tính bán kính của đường tròn ngoại tiếp tam giác ABC.

Sử dụng định lý Pythagore đảo chứng minh tam giác ABC vuông tại A, suy ra bán kính đường tròn ngoại tiếp tam giác ABC là: \(\frac{{BC}}{2}\).

Vì \(A{B^2} + A{C^2} = B{C^2}\left( {do\;{3^2} + {4^2} = {5^2}} \right)\) nên tam giác ABC vuông tại A (định lý Pythagore đảo)
Do đó, bán kính đường tròn tròn ngoại tiếp tam giác ABC là: \(R = \frac{{BC}}{2} = \frac{5}{2}\left( {cm} \right)\).
Hoạt động (HĐ) 4
Trả lời câu hỏi Hoạt động 4 trang 73SGK Toán 9
a) Vẽ tam giác đều ABC. Hãy trình bày cách xác định tâm của đường tròn ngoại tiếp tam giác ABC và vẽ đường tròn đó.
b) Giải thích vì sao tâm O của đường tròn ngoại tiếp tam giác ABC trùng với trọng tâm của tam giác đó (H.9.17).
c) Giải thích vì sao \(\widehat {OBM} = {30^o}\) và \(OB = \frac{{\sqrt 3 }}{3}BC\) (với M là trung điểm của BC).
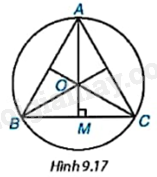

a) Kẻ ba đường trung trực của các cạnh AB, AC, BC. Gọi O là giao điểm của ba đường trung trực đó thì O là tâm của đường tròn ngoại tiếp tam giác ABC.
b) + Trong tam giác đều, giao điểm của ba đường trung trực đồng thời là trọng tâm của tam giác đó.
+ Suy ra, tâm O đường tròn ngoại tiếp trùng với trọng tâm của tam giác đó.
c) Gọi E là giao điểm của BO và AC.
+ Chứng minh BE là đường phân giác và trung tuyến của tam giác đều ABC.
Do đó, \(OB = \frac{2}{3}BE\), \(\widehat {OBM} = {30^o}\)
+ Áp dụng định lý Pythagore vào tam giác BEC để tính BE, từ đó tính OB.

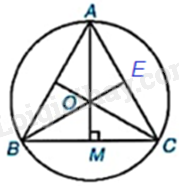
a) Kẻ ba đường trung trực của các cạnh AB, AC, BC. Gọi O là giao điểm của ba đường trung trực đó thì O là tâm của đường tròn ngoại tiếp tam giác ABC.
b) Vì tam giác ABC đều nên O vừa là giao điểm của ba đường trung trực trong tam giác, vừa là trọng tâm của tam giác. Do đó, tâm O của đường tròn ngoại tiếp tam giác ABC trùng với trọng tâm của tam giác đó.
c) Tam giác ABC đều nên \(BC = AC,\widehat {ABC} = {60^o}\)
Gọi E là giao điểm của BO và AC. Khi đó, BE là đường trung trực của tam giác ABC.
Vì tam giác ABC đều nên BE là đường trung trực, đường trung tuyến và đường phân giác của tam giác.
Do đó, \(OB = \frac{2}{3}BE\) và \(\widehat {OBM} = \frac{1}{2}\widehat {ABC} = \frac{1}{2}{.60^o} = {30^o}\).
Vì E là trung điểm của AC nên \(EC = \frac{{AC}}{2} = \frac{{BC}}{2}\).
Tam giác BEC vuông tại E nên theo định lý Pythagore ta có:
\(B{E^2} + E{C^2} = B{C^2}\)
\(BE = \sqrt {B{C^2} - E{C^2}} = \sqrt {B{C^2} - {{\left( {\frac{{BC}}{2}} \right)}^2}} = \frac{{BC\sqrt 3 }}{2}\)
\(OB = \frac{2}{3}.\frac{{BC\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{3}BC\)
Luyện tập (LT) 2
Giải câu hỏi Luyện tập 2 trang 74 SGK Toán 9
Cho tam giác đều ABC nội tiếp đường tròn (O) có bán kính bằng 4cm. Tính độ dài các cạnh của tam giác ABC.

+ Vì tam giác ABC đều nội tiếp đường tròn (O) nên O là trọng tâm, trực tâm của tam giác ABC.
+ Gọi H là giao điểm của AO và BC nên AH là trung trực đồng thời là đường cao trong tam giác đều ABC. Do đó: \(OA = \frac{{BC\sqrt 3 }}{3}\), từ đó tính được BC.

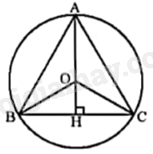
Vì tam giác ABC đều nội tiếp đường tròn (O) nên O là trọng tâm, trực tâm của tam giác ABC.
Gọi H là giao điểm của AO và BC nên AH là trung trực đồng thời là đường cao trong tam giác đều ABC.
Do đó: \(OA = \frac{{BC\sqrt 3 }}{3} \Rightarrow BC = \sqrt 3 OA = 4\sqrt 3 \left( {cm} \right)\).
Vậy cạnh của tam giác đều bằng \(4\sqrt 3 cm\).
