Hoạt động (HĐ) 5
Trả lời câu hỏi Hoạt động 5 trang 74SGK Toán 9
Cho tam giác ABC có ba đường phân giác đồng quy tại điểm I. Gọi D, E, F lần lượt là chân các đường vuông góc kẻ từ I xuống các cạnh BC, CA và AB (H.9.19).
a) Hãy giải thích vì sao các điểm D, E, F cùng nằm trên một đường tròn có tâm I.
b) Gọi (I) là đường tròn trên. Hãy giải thích vì sao (I) tiếp xúc với các cạnh của tam giác ABC.
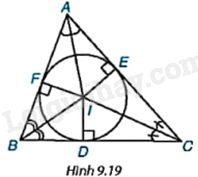

a) Sử dụng tính chất: Giao điểm của ba đường phân giác trong tam giác cách đều ba cạnh của tam giác, do đó \(IE = ID = FI\).
b) Vì \(IE \bot AC\left( {E \in AC} \right),IE = R\) nên AC tiếp xúc với đường tròn (I; R) tại E, tương tự ta chứng minh được đường tròn (I) tiếp xúc với các cạnh của tam giác ABC.

a) Vì D, E, F lần lượt là chân các đường vuông góc kẻ từ I xuống các cạnh BC, CA và AB nên \(IF \bot AB,IE \bot AC,ID \bot BC\).
Vì I là giao điểm của ba đường phân giác nên I cách đều ba cạnh AB, AC, CB. Do đó, \(IE = IF = ID\)
Do đó, ba điểm D, E, F cùng nằm trên một đường tròn có tâm I.
b) Gọi \(IE = IF = ID = R\) nên ba điểm D, E, F cùng nằm trên đường tròn (I; R).
Vì \(IE \bot AC\left( {E \in AC} \right),IE = R\) nên AC tiếp xúc với đường tròn (I; R) tại E.
Vì \(IF \bot AB\left( {F \in AB} \right),IF = R\) nên AB tiếp xúc với đường tròn (I; R) tại F.
Vì \(ID \bot BC\left( {D \in BC} \right),ID = R\) nên BC tiếp xúc với đường tròn (I; R) tại D.
Vậy đường tròn (I) ở trên tiếp xúc với các cạnh của tam giác ABC.
Câu hỏi
Gợi ý giải câu hỏi Câu hỏi trang 75SGK Toán 9
Mỗi tam giác có bao nhiêu đường tròn nội tiếp? Có bao nhiêu tam giác cùng ngoại tiếp một đường tròn?

Mỗi tam giác có một đường tròn nội tiếp. Có một tam giác ngoại tiếp một đường tròn.

Mỗi tam giác có một đường tròn nội tiếp. Có một tam giác ngoại tiếp một đường tròn.
Hoạt động (HĐ) 6
Đáp án câu hỏi Hoạt động 6 trang 75SGK Toán 9
Cho tam giác ABC đều có trọng tâm G.
a) Giải thích vì sao G cũng là tâm đường tròn nội tiếp tam giác ABC.
b) Từ đó, giải thích vì sao bán kính đường tròn nội tiếp tam giác ABC bằng một nửa đường tròn ngoại tiếp tam giác ABC và bằng \(\frac{{\sqrt 3 }}{6}BC\).

a) Sử dụng tính chất: Trong tam giác đều, trọng tâm đồng thời là giao điểm của ba đường phân giác. Suy ra, G là tâm đường tròn nội tiếp tam giác ABC.
b) + Gọi D là giao điểm của AG và CB. Khi đó, GD là bán kính đường tròn đường tròn nội tiếp tam giác ABC, AG là bán kính đường tròn ngoại tiếp tam giác ABC.
Advertisements (Quảng cáo)
+ Theo tính chất của trọng tâm trong tam giác ABC ta có: \(GD = \frac{1}{2}AG = \frac{1}{3}AD\).
+ Theo định lý Pythagore vào tam giác ADC vuông tại D tính được: \(AD = \frac{{BC\sqrt 3 }}{2}\), nên \(GD = \frac{{\sqrt 3 }}{6}BC\).

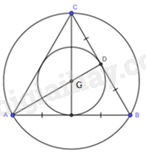
a) Tam giác ABC đều nên G là trọng tâm của tam giác ABC đồng thời là giao điểm của ba đường phân giác. Do đó, G là tâm đường tròn nội tiếp tam giác ABC.
b) Vì G là giao điểm của ba đường trung trực trong tam giác đều ABC (do G là trọng tâm tam giác ABC) nên G là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi D là giao điểm của AG và CB. Suy ra, AG là bán kính đường tròn ngoại tiếp tam giác ABC.
Tam giác ABC đều nên AD là đường trung tuyến đồng thời là đường cao trong tam giác. Do đó, \(GD \bot CB\) tại D. Suy ra, GD là bán kính đường tròn nội tiếp tam giác ABC.
Vì G là trọng tâm tam giác ABC nên \(GD = \frac{1}{2}AG = \frac{1}{3}AD\).
Áp dụng định lý Pythagore vào tam giác ADC vuông tại D có:
\(A{D^2} + C{D^2} = A{C^2} \Rightarrow AD = \sqrt {A{C^2} - C{D^2}} = \sqrt {B{C^2} - \frac{{B{C^2}}}{4}} = \frac{{BC\sqrt 3 }}{2}\)
Do đó, \(GD = \frac{1}{3}.\frac{{BC\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{6}BC\).
Vậy bán kính đường tròn nội tiếp tam giác ABC bằng một nửa đường tròn ngoại tiếp tam giác ABC và bằng \(\frac{{\sqrt 3 }}{6}BC\).
Luyện tập (LT) 3
Giải câu hỏi Luyện tập 3 trang 76SGK Toán 9
Cho tam giác đều ABC (H.9.22).
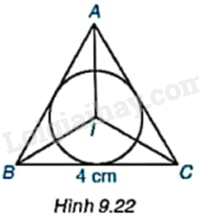
a) Vẽ đường tròn (I; r) nội tiếp tam giác ABC.
b) Biết rằng \(BC = 4cm\), hãy tính bán kính r.

a) + Vẽ ba đường phân giác của tam giác ABC.
+ Gọi I là giao điểm của ba đường phân giác đó.
+ Gọi H là giao điểm của AI và BC. Vẽ đường tròn tâm I, bán kính IH.
+ Khi đó, đường tròn (I; IH) là đường tròn nội tiếp tam giác ABC cần vẽ.
b) Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{6}a\)

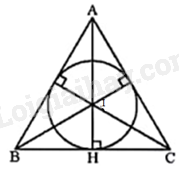
a) Vẽ ba đường phân giác của tam giác ABC. Gọi I là giao điểm của ba đường phân giác đó.
Gọi H là giao điểm của AI và BC. Vẽ đường tròn tâm I, bán kính IH.
Khi đó, đường tròn (I; IH) là đường tròn nội tiếp tam giác ABC cần vẽ.
b) Vì (I; r) nội tiếp tam giác ABC nên bán kính đường tròn nội tiếp tam giác ABC là:
\(r = \frac{{BC\sqrt 3 }}{6} = \frac{{4\sqrt 3 }}{6} = \frac{{2\sqrt 3 }}{3}\left( {cm} \right)\)
