Hoạt động (HĐ) 1
Hướng dẫn giải câu hỏi Hoạt động 1 trang 80SGK Toán 9
Cho tứ giác ABCD có \(\widehat A = \widehat C = {90^o}\) (H.9.28). Hãy giải thích vì sao bốn đỉnh của tứ giác ABCD cùng nằm trên một đường tròn có tâm là trung điểm O của đoạn thẳng BD.
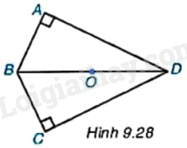

+ Do tam giác ABD vuông tại A nên ba điểm A, B, D thuộc đường tròn đường kính BD với trung điểm của BD là tâm.
+ Vì tam giác CBD vuông tại C nên ba điểm C, B, D thuộc đường tròn đường kính BD với trung điểm của BD là tâm.

Vì tam giác ABD vuông tại A nên ba điểm A, B, D thuộc đường tròn đường kính BD. Mà O là trung điểm của BD nên ba điểm A, B, D thuộc đường tròn (O).
Vì tam giác CBD vuông tại C nên ba điểm C, B, D thuộc đường tròn đường kính BD. Mà O là trung điểm của BD nên ba điểm C, B, D thuộc đường tròn (O).
Do đó, 4 đỉnh của tứ giác ABCD cùng nằm trên một đường tròn có tâm là trung điểm O của BD.
Hoạt động (HĐ) 2
Trả lời câu hỏi Hoạt động 2 trang 80SGK Toán 9
Trên đường tròn (O), lấy các điểm A, B, C, D sao cho tứ giác ABCD là tứ giác lồi (H.9.29). Các đường trung trực của các cạnh AB, BC, CD, DA có đồng quy hay không?
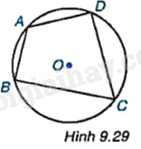

+ Gọi E là trung điểm của AD.
+ Chứng minh được OE là đường trung trực của AD.
+ Chứng minh tương tự ta có các đường trung trực của các cạnh AB, BC, CD cũng đi qua O.
+ Vậy các đường trung trực của các cạnh AB, BC, CD, DA có đồng quy.

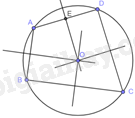
Gọi E là trung điểm của AD. Tam giác AOD cân tại O (do \(OA = OD\)) nên OE là đường trung tuyến đồng thời là đường cao trong tam giác. Do đó, \(OE \bot AD\) tại E.
Vì \(OE \bot AD\) tại E và E là trung điểm của AD nên OE là đường trung trực của AD.
Do đó, đường trung trực của đoạn thẳng AD đi qua O.
Chứng minh tương tự ta có: Các đường trung trực của các cạnh AB, BC, CD đi qua O.
Vậy các đường trung trực của các cạnh AB, BC, CD, DA có đồng quy.
Hoạt động (HĐ) 3
Giải câu hỏi Hoạt động 3 trang 81 SGK Toán 9
Em hãy đo các góc đối nhau A và C của tứ giác ABCD trong HĐ2 và tính tổng \(\widehat A + \widehat C\). So sánh kết quả của em với các bạn.
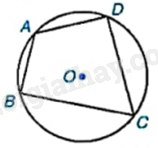

Sử dụng thước đo góc để đo các góc A và C rồi tính tổng \(\widehat A + \widehat C\).

Advertisements (Quảng cáo)
Ta có: \(\widehat A = {115^o},\widehat C = {65^o}\) và \(\widehat A + \widehat C = {65^o} + {115^o} = {180^o}\)
Luyện tập (LT) 1
Giải câu hỏi Luyện tập 1 trang 81 SGK Toán 9
Cho tam giác ABC có các đường cao BE, CF. Biết rằng \(\widehat B = {60^o},\widehat C = {80^o}\).
a) Chứng tỏ rằng tứ giác BCEF nội tiếp một đường tròn có tâm là trung điểm của cạnh BC.
b) Tính số đo của các góc BFE và CEF.

a) + Chứng minh các tam giác BEC và tam giác BFC là các tam giác vuông.
+ Suy ra, các điểm B, F, E, C cùng thuộc đường tròn đường kính BC với tâm là trung điểm của BC.
b) Vì tứ giác BFEC nội tiếp đường tròn đường kính BC nên \(\widehat {FBC} + \widehat {FEC} = {180^o},\widehat {ECB} + \widehat {BFE} = {180^o}\), từ đó tính được các góc BFE và CEF.

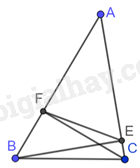
a) Vì BE, CF là các đường cao của tam giác ABC nên \(BE \bot AC,CF \bot AB\). Do đó, tam giác BFC vuông tại F và tam giác BEC vuông tại E.
Vì tam giác BFC vuông tại F nên ba điểm B, F, C thuộc đường tròn đường kính BC với tâm là trung điểm của BC.
Vì tam giác BEC vuông tại E nên ba điểm B, E, C thuộc đường tròn đường kính BC với tâm là trung điểm của BC.
Vậy tứ giác BCEF nội tiếp một đường tròn có tâm là trung điểm của cạnh BC.
b) Vì tứ giác BFEC nội tiếp đường tròn đường kính BC nên
+ \(\widehat {FBC} + \widehat {FEC} = {180^o}\), hay \(\widehat {FEC} = {180^o} - \widehat {FBC} = {180^o} - {60^o} = {120^o}\).
+ \(\widehat {ECB} + \widehat {BFE} = {180^o}\), hay \(\widehat {BFE} = {180^o} - \widehat {ECB} = {180^o} - {80^o} = {100^o}\).
Thử thách nhỏ (TTN) 1
Giải câu hỏi Thử thách nhỏ 1 trang 82 SGK Toán 9
Cho tứ giác ABCD, biết rằng các đường trung trực của ba đoạn thẳng AB, AC, AD đồng quy tại một điểm. Hãy giải thích vì sao ABCD là tứ giác nội tiếp.

+ Gọi O là giao điểm của các đường trung trực của ba đoạn thẳng AB, AC, AD.
+ Sử dụng tính chất đường trung trực chứng minh được \(OA = OB = OC = OD\).
+ Suy ra, bốn điểm A, B, C, D cùng thuộc một đường tròn. Vậy ABCD là tứ giác nội tiếp.

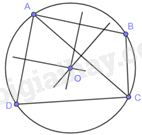
Gọi O là giao điểm của các đường trung trực của ba đoạn thẳng AB, AC, AD.
Vì O thuộc trung trực của AB nên \(OA = OB\).
Vì O thuộc trung trực của AC nên \(OA = OC\).
Vì O thuộc trung trực của AD nên \(OA = OD\).
Do đó, \(OA = OB = OC = OD\).
Suy ra, bốn điểm A, B, C, D cùng thuộc đường tròn (O). Vậy ABCD là tứ giác nội tiếp.
