Hoạt động (HĐ) 1
Trả lời câu hỏi Hoạt động 1 trang 84 SGK Toán 9
Ta đã biết các tam giác đều và hình vuông có các đỉnh nằm trên một đường tròn. Ta dựng một đa giác lồi 5 cạnh có các đỉnh nằm trên một đường tròn như sau:
- Vẽ đường tròn tâm O bán kính R.
- Lần lượt lấy các điểm A, B, C, D, E trên đường tròn theo thứ tự ngược chiều kim đồng hồ (hoặc theo chiều kim đồng hồ) sao cho: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA} = \frac{{{{360}^o}}}{5} = {72^o}\).
Em hãy giải thích vì sao các cạnh và các góc của đa giác ABCDE bằng nhau (H.9.39).
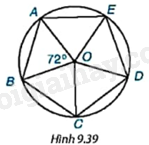

+ Chứng minh được các tam giác \(\Delta EOA = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.g.c} \right)\)
Suy ra: \(AE = ED = DC = CB = BA\) và
\(\widehat {OAE} = \widehat {OEA} = \widehat {ODE} = \widehat {OED} = \widehat {ODC} = \widehat {OCD} = \widehat {OCB} = \widehat {OBC} = \widehat {OBA} = \widehat {OAB}\)
+ Suy ra: \(\widehat {BAE} = \widehat {AED} = \widehat {EDC} = \widehat {DCB} = \widehat {CBA}\)

Vì đa giác ABCDE nội tiếp đường tròn (O) nên \(OA = OB = OC = OD = OE\).
Theo giả thiết: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA} = {72^o}\)
Do đó, \(\Delta EOA = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.g.c} \right)\).
Suy ra:
+) \(AE = ED = DC = CB = BA\)
+) \(\widehat {OAE} = \widehat {OEA} = \widehat {ODE} = \widehat {OED} = \widehat {ODC} = \widehat {OCD} = \widehat {OCB} = \widehat {OBC} = \widehat {OBA} = \widehat {OAB}\)
Do đó, \(\widehat {OAE} + \widehat {OAB} = \widehat {OEA} + \widehat {OED} = \widehat {ODE} + \widehat {ODC} = \widehat {OCD} + \widehat {OCB} = \widehat {OBC} + \widehat {OBA}\)
Suy ra: \(\widehat {BAE} = \widehat {AED} = \widehat {EDC} = \widehat {DCB} = \widehat {CBA}\).
Vậy các cạnh và các góc của đa giác ABCDE bằng nhau.
Câu hỏi
Đáp án câu hỏi Câu hỏi trang 85 SGK Toán 9
Nếu một lục giác đều (đa giác đều 6 cạnh) nội tiếp một đường tròn bán kính 2cm (H.9.40) thì độ dài các cạnh của lục giác đều đó bằng bao nhiêu centimét? Số đo các góc của lục giác đều bằng bao nhiêu độ?
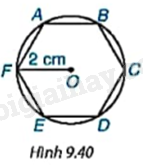

+ Chứng minh \(\Delta AOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\), suy ra
\(\widehat {FOA} = \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \frac{{{{360}^o}}}{6} = {60^o}\)
+ Chứng minh tam giác AOB đều, từ đó tính được AB và \(\widehat {OAB} = \widehat {OBA} = {60^o}\).
+ Tính được \(\widehat {FAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFA} = {120^o}\).

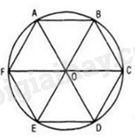
Vì ABCDEF là lục giác đều \(AB = BC = CD = DE = EF = FA\).
Mà lục giác ABCDEF nội tiếp đường tròn (O) nên \(OA = OB = OC = OD = OE = OF\).
Do đó, \(\Delta AOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\)
Do đó,
+) \(\widehat {FOA}\)\( = \widehat {AOB}\)\( = \widehat {BOC}\)\( = \widehat {COD}\)\( = \widehat {DOE}\)\( = \widehat {EOF}\)\( = \frac{{{{360}^o}}}{6}\)\( = {60^o}\)
+) \(\widehat {OAF}\)\( = \widehat {OFA}\)\( = \widehat {OEF}\)\( = \widehat {OFE}\)\( = \widehat {ODE}\)\( = \widehat {OED}\)\( = \widehat {ODC}\)\( = \widehat {OCD}\)\( = \widehat {OCB}\)\( = \widehat {OBC}\)\( = \widehat {OBA}\)\( = \widehat {OAB}\)
Tam giác AOB có: \(OA = OB,\widehat {AOB} = {60^o}\) nên tam giác OAB đều.
Do đó, \(OA = AB = 2cm\) và \(\widehat {OAB} = \widehat {OBA} = {60^o}\)
Suy ra:
\(\widehat {OAF} + \widehat {OAB}\)\( = \widehat {OFA} + \widehat {OFE}\)\( = \widehat {OEF} + \widehat {OED}\)\( = \widehat {ODE} + \widehat {ODC}\)\( = \widehat {OCD} + \widehat {OCB}\)\( = \widehat {OBC} + \widehat {OBA}\)\( = {60^o} + {60^o}\)\( = {120^o}\)
Do đó: \(\widehat {FAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFA} = {120^o}\)
Vậy lục giác đều ABCDEF nội tiếp (O) bán kính 2cm có độ dài cạnh bằng 2cm và số đo các góc lục giác đều bằng \({120^o}\)
Advertisements (Quảng cáo)
Luyện tập (LT) 1
Giải câu hỏi Luyện tập 1 trang 86 SGK Toán 9
Cho M, N, P, Q, K lần lượt là trung điểm của các cạnh AB, BC, CD, DE và EA của ngũ giác đều ABCDE (H.9.44). Hỏi MNPQK có phải là ngũ giác đều hay không?
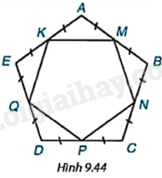

+ Chứng minh \(\Delta AMK = \Delta BMN = \Delta CPN = \Delta DPQ = \Delta EKQ\left( {c.g.c} \right)\) nên \(KM = MN = PN = PQ = QK\).
+ Chứng minh được \(\widehat {KMA} = \widehat {BMN}\) và \(\widehat {KMA} + \widehat {KMN} + \widehat {BMN} = {180^o} \Rightarrow \widehat {KMN} = {180^o} - 2\widehat {KMA}\).
+ Chứng minh tương tự ta có: \(\widehat {NPQ} = \widehat {PQK} = \widehat {QKM} = {180^o} - 2\widehat {KMA}\). Do đó, đa giác MNPQK là ngũ giác đều.

Vì ABCDE là ngũ giác đều nên \(AB = BC = CD = DE = EA\), \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E\)
Vì M, N, P, Q, K lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EA.
Do đó, \(AM = MB = NB = NC = CP = PD = DQ = QE = EK = KA\)
Ta có: \(AM = MB = NB = NC = CP = PD = DQ = QE = EK = KA\) và \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E\)
Suy ra: \(\Delta AMK = \Delta BMN = \Delta CPN = \Delta DPQ = \Delta EKQ\left( {c.g.c} \right)\)
Do đó: + \(KM = MN = PN = PQ = QK\left( 1 \right)\).
+ \(\widehat {KMA} = \widehat {AKM} = \widehat {BMN} = \widehat {MNB} = \widehat {CNP} = \widehat {CPN} = \widehat {DPQ} = \widehat {DQP} = \widehat {EQK} = \widehat {EKQ}\)
Ta có: \(\widehat {KMA} + \widehat {KMN} + \widehat {BMN} = {180^o}\) (các góc kề bù)
Mà \(\widehat {KMA} = \widehat {BMN}\) nên \(\widehat {KMN} = {180^o} - 2\widehat {KMA}\).
Vì \(\widehat {BNM} + \widehat {MNP} + \widehat {PNC} = {180^o}\) (các góc kề bù)
Mà \(\widehat {KMA} = \widehat {BNM} = \widehat {PNC}\) nên \(\widehat {MNP} = {180^o} - 2\widehat {KMA}\).
Chứng minh tương tự ta có:
\(\widehat {NPQ} = \widehat {PQK} = \widehat {QKM} = {180^o} - 2\widehat {KMA}\)
Do đó, \(\widehat {KMN} = \widehat {MNP} = \widehat {NPQ} = \widehat {PQK} = \widehat {QKM}\left( 2 \right)\)
Từ (1) và (2) suy ra: MNPQK là ngũ giác đều.
Thử thách nhỏ (TTN) 1
Gợi ý giải câu hỏi Thử thách nhỏ 1 trang 87SGK Toán 9
Cho một bát giác đều (đa giác đều 8 cạnh) nội tiếp một đường tròn tâm O (H.9.45). Hỏi mỗi góc của bát giác đều có số đo bằng bao nhiêu?
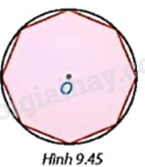

+ Gọi ABCDEFGH là bát giác đều nội tiếp đường tròn (O).
+ Chứng minh \(\Delta AOH = \Delta GOH = \Delta GOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\), suy ra: \(\widehat {HOA} = \widehat {HOG} = \widehat {GOF} = \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \frac{{{{360}^o}}}{8} = {45^o}\)
+ Tính được: \(\widehat {OAB} = \widehat {OBA} = \frac{{{{180}^o} - \widehat {AOB}}}{2} = 67,{5^o}\)
+ Do đó \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFG} = \widehat {FGH} = \widehat {GHA} = {135^o}\)

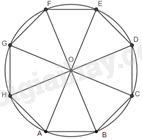
Gọi ABCDEFGH là bát giác đều nội tiếp đường tròn (O).
Vì ABCDEFGH là bát giác đều nên \(AB = BC = CD = DE = EF = FG = GH = HA\).
Vì ABCDEFGH là bát giác đều nội tiếp (O) nên \(OA = OB = OC = OD = OE = OF = OH = OG\).
Do đó, \(\Delta AOH = \Delta GOH = \Delta GOF = \Delta EOF = \Delta EOD = \Delta COD = \Delta COB = \Delta AOB\left( {c.c.c} \right)\)
Suy ra: \(\widehat {HOA} = \widehat {HOG} = \widehat {GOF} = \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \frac{{{{360}^o}}}{8} = {45^o}\)
Tam giác AOB cân tại O (do \(OA = OB\)) nên \(\widehat {OAB} = \widehat {OBA}\).Do đó, \(\widehat {OAB} = \widehat {OBA} = \frac{{{{180}^o} - \widehat {AOB}}}{2} = 67,{5^o}\)
Chứng minh tương tự ta có:
\(\widehat {OBC} = \widehat {OCB} = \widehat {ODE} = \widehat {OED} = \widehat {OEF} = \widehat {OFE} = \widehat {OFG} = \widehat {OGF} = \widehat {OGH} = \widehat {OHG} = \widehat {OHA} = \widehat {OAH} = 67,{5^o}\)
Suy ra \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEF} = \widehat {EFG} = \widehat {FGH} = \widehat {GHA} = {135^o}\).
Vậy mỗi góc của bát giác đều bằng \({135^o}\).
