Câu hỏi/bài tập:

Người ta muốn làm một khay đựng bánh kẹo hình lục giác đều có cạnh 10cm và chia thành 7 ngăn gồm một lục giác đều nhỏ và 6 hình thang cân như Hình 9.60. Hỏi lục giác đều nhỏ phải có cạnh bằng bao nhiêu để nó có diện tích bằng hai lần diện tích mỗi hình thang?

+ Xét khay đựng bánh kẹo hình lục giác đều ABCDEH có cạnh bằng 10cm.
+ Hình lục giác đều ABCDEH gồm 6 hình thang ABQP, BCMQ, CDNM, EDNR, TREH, HTPA và hình lục giác đều PQMNRT.
+ Gọi độ dài cạnh lục giác đều PQMNRT bằng x (cm, \(0 < x < 10\))
+ Vì lục giác đều PQMNRT chia thành 6 tam giác đều OPQ, OQM, OMN, ONR, ORT, OPT bằng nhau nên \({S_{PQMNRT}} = 6{S_{\Delta OPQ}} = 6.\frac{{{x^2}\sqrt 3 }}{4} = \frac{{3{x^2}\sqrt 3 }}{2}\left( {c{m^2}} \right)\).
+ Kẻ \(OL \bot AB\) tại L, I là giao điểm của OL và PQ. Khi đó, OL là chiều cao của tam giác OAB, OI là chiều cao của tam giác OPQ.
Tính được \(IL = OL - OI = \frac{{10\sqrt 3 - x\sqrt 3 }}{2}\left( {cm} \right)\).
+ Diện tích hình thang ABQP là: \(\frac{{\left( {10 + x} \right)\left( {10\sqrt 3 - x\sqrt 3 } \right)}}{4}\left( {c{m^2}} \right)\)
+ Phương trình: \(\frac{{3{x^2}\sqrt 3 }}{2} = 2.\frac{{\left( {10 + x} \right)\left( {10\sqrt 3 - x\sqrt 3 } \right)}}{4}\), giải phương trình tìm x, đối chiếu điều kiện đưa ra kết luận.

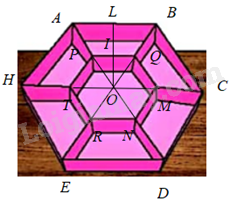
Xét khay đựng bánh kẹo hình lục giác đều ABCDEH có cạnh bằng 10cm.
Hình lục giác đều ABCDEH gồm 6 hình thang ABQP, BCMQ, CDNM, EDNR, TREH, HTPA và hình lục giác đều PQMNRT.
Advertisements (Quảng cáo)
Gọi độ dài cạnh lục giác đều PQMNRT bằng x (cm, \(0 < x < 10\))
Lục giác đều PQMNRT chia thành 6 tam giác đều OPQ, OQM, OMN, ONR, ORT, OPT bằng nhau.
Do đó, \({S_{PQMNRT}} = 6{S_{\Delta OPQ}} = 6.\frac{{{x^2}\sqrt 3 }}{4} = \frac{{3{x^2}\sqrt 3 }}{2}\left( {c{m^2}} \right)\).
Kẻ \(OL \bot AB\) tại L, I là giao điểm của OL và PQ. Khi đó, OL là chiều cao của tam giác OAB, OI là chiều cao của tam giác OPQ.
Lục giác đều ABCDEH chia thành 6 tam giác đều AOB, BOC, COD, DOE, EOH, HOA bằng nhau có cạnh bằng 10cm.
Tam giác AOB đều cạnh bằng 10cm, chiều cao OL nên \(OL = \frac{{10\sqrt 3 }}{2}\left( {cm} \right)\)
Tam giác OPQ đều cạnh bằng x, chiều cao OI nên \(OI = \frac{{x\sqrt 3 }}{2}\left( {cm} \right)\)
Do đó, \(IL = OL - OI = \frac{{10\sqrt 3 - x\sqrt 3 }}{2}\left( {cm} \right)\)
Hình thang ABQP có đáy lớn \(AB = 10cm,\) đáy nhỏ \(PQ = x\left( {cm} \right)\), chiều cao \(IL = \frac{{10\sqrt 3 - x\sqrt 3 }}{2}\left( {cm} \right)\) nên diện tích hình thang ABQP là:
\(\frac{{\left( {10 + x} \right)\left( {10\sqrt 3 - x\sqrt 3 } \right)}}{4}\left( {c{m^2}} \right)\).
Vì diện tích lục giác đều PQMNRT gấp 2 lần diện tích hình thang ABQP nên
\(\frac{{3{x^2}\sqrt 3 }}{2} = 2.\frac{{\left( {10 + x} \right)\left( {10\sqrt 3 - x\sqrt 3 } \right)}}{4}\)
\(\left( {10 + x} \right)\left( {10 - x} \right) = 3{x^2}\)
\(100 - {x^2} = 3{x^2}\)
\(x = 5\left( {do\;0 < x < 10} \right)\)
Vậy hình lục giác nhỏ có cạnh bằng 5cm thì diện tích bằng 2 lần diện tích mỗi hình thang.
