Câu hỏi/bài tập:
Vẽ đường tròn tâm O có bán kính bằng 2cm và dây cung AB có độ dài bằng 2cm. Lấy một điểm C tùy ý nằm trên cung lớn AmB (H.9.2).
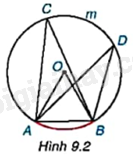
a) Cho biết số đo góc ở tâm AOB và số đo của cung bị chắn AB.
b) Đo góc ACB và so sánh với kết quả của bạn bên cạnh.
c) Lấy điểm D tùy ý nằm trên cung ACB. Đo góc ADB và so sánh với các góc ACB và AOB.

a) Chứng minh tam giác AOB đều, suy ra \(\widehat {AOB} = {60^o}\). Do đó, \(sđ\overset\frown{AB}=\widehat{AOB}={{60}^{o}}\) (góc ở tâm chắn cung AB).
Advertisements (Quảng cáo)
b, c) Sử dụng thước đo góc đo được góc ACB, góc ADB đều bằng 30 độ. Do đó, \(\widehat {ACB} = \widehat {ADB}\)

Vì A, B thuộc đường tròn tâm O nên \(OA = OB = 2cm\).
Tam giác AOB có: \(OA = OB = AB = 2cm\) nên tam giác ABO đều.
Do đó, \(\widehat {AOB} = {60^o}\).
Suy ra: \(sđ\overset\frown{AB}=\widehat{AOB}={{60}^{o}}\) (góc ở tâm chắn cung AB).
b) Sử dụng thước đo góc, ta đo được \(\widehat {ACB} = {30^o}\).
c) Sử dụng thước đo góc, ta đo được \(\widehat {ADB} = {30^o}\). Do đó, \(\widehat {ACB} = \widehat {ADB}\).
