Câu hỏi/bài tập:
Cho hình thoi ABCD có các cạnh bằng 3cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, AD. Chứng tỏ rằng tứ giác MNPQ là hình chữ nhật và tìm bán kính đường tròn ngoại tiếp của tứ giác đó.

+ Sử dụng tính chất đường trung bình trong tam giác chứng minh được: MN//AC, PQ//AC, \(MN = PQ = \frac{1}{2}AC\) nên tứ giác MNPQ là hình bình hành.
+ Chứng minh được MQ//BD, MN//AC, \(BD \bot AC\) nên \(MQ \bot MN\) nên \(\widehat {QMN} = {90^o}\).
+ Chứng minh tứ giác MNPQ là hình chữ nhật.
+ Áp dụng định lý Pythagore vào tam giác MNQ vuông tại M để tính NQ, từ đó tính được bán kính đường tròn ngoại tiếp tứ giác MNPQ.

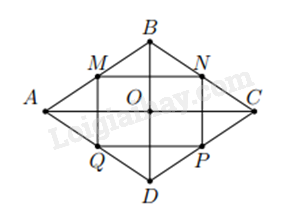
Vì M, N lần lượt là trung điểm của AB, BC nên MN là đường trung bình của tam giác ABC. Do đó, MN//AC, \(MN = \frac{1}{2}AC\) (1).
Vì M, Q lần lượt là trung điểm của AB, AD nên MQ là đường trung bình của tam giác ABD. Do đó, MQ//BD, \(MQ = \frac{1}{2}BD\).
Advertisements (Quảng cáo)
Vì P, Q lần lượt là trung điểm của DC, AD nên PQ là đường trung bình của tam giác ADC. Do đó, PQ//AC, \(PQ = \frac{1}{2}AC\) (2).
Từ (1) và (2) ta có: \(MN = PQ\) và MN//PQ nên tứ giác MNPQ là hình bình hành (3).
Vì MN//AC, \(AC \bot BD\) (do ABCD là hình thoi) nên \(MN \bot BD\)
Vì MQ//BD, \(MN \bot BD\) nên \(MQ \bot MN \Rightarrow \widehat {QMN} = {90^o}\) (4)
Từ (3) và (4) ta có: Tứ giác MNPQ là hình chữ nhật.
Gọi O là giao điểm của AC và BD.
Vì ABCD là hình thoi nên \(AC \bot BD\) tại O và \(OB = \frac{1}{2}BD,OC = \frac{1}{2}AC\). Do đó, \(MN = OC,MQ = OB\).
Áp dụng định lý Pythagore vào tam giác BOC vuông tại O có: \(O{B^2} + O{C^2} = 9\). Do đó, \(M{N^2} + M{Q^2} = 9\)
Áp dụng định lý Pythagore vào tam giác MNQ vuông tại M có:
\(N{Q^2} = M{N^2} + M{Q^2} = 9 \Rightarrow NQ = \sqrt 9 = 3\left( {cm} \right)\)
Vì MNPQ là hình chữ nhật nên đường tròn ngoại tiếp tứ giác MNPQ có bán kính là \(\frac{{NQ}}{2} = \frac{3}{2}\left( {cm} \right)\).
