Sử dụng định lí về mối quan hệ giữa góc nội tiếp và cung bị chắn để chứng minh. Hướng dẫn giải Câu hỏi Luyện tập trang 70 SGK Toán 9 Kết nối tri thức - Bài 27. Góc nội tiếp.
Câu hỏi/bài tập:
Cho đường tròn tâm O và hai dây cung AB, CD cắt nhau tại điểm X nằm trong đường tròn (H.9.6). Chứng minh rằng $\Delta AXC\backsim \Delta DXB$.
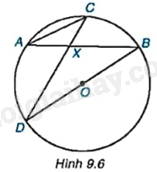

+ Sử dụng định lý về mối quan hệ giữa góc nội tiếp và cung bị chắn để chứng minh \(\widehat {ACX} = \widehat {XBD}\).
Advertisements (Quảng cáo)
+ Chứng minh $\Delta AXC\backsim \Delta DXB$ theo trường hợp góc – góc.

Vì góc ACX và góc XBD là góc nội tiếp cùng chắn cung AD của đường tròn tâm O nên: \(\widehat {ACX} = \widehat {XBD}\).
Tam giác AXC và tam giác DXB có: \(\widehat {ACX} = \widehat {XBD}\) (cmt), \(\widehat {AXC} = \widehat {BXD}\) (hai góc đối đỉnh).
Do đó, $\Delta AXC\backsim \Delta DXB$ (g – g).
