
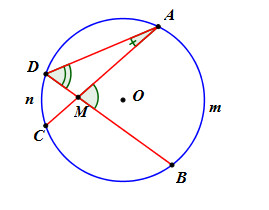
Nhìn hình vẽ, hãy điền vào ô trống theo mẫu:
|
Đẳng thức |
Diễn giải |
|
\(\)\(\widehat {AMB} = \widehat {ADB} + \widehat {CAD}\) |
Góc ngoài của \(\Delta AMD\) |
|
\(\widehat {ADB} = \dfrac{{sd\,cung\,AB}}{2}\) |
|
|
\(\widehat {CAD} = \dfrac{{sd\,cung\,CD}}{2}\)\(\) |
|
|
\(\widehat {AMB} = \dfrac{{sd\,cung\,AB + sd\,cung\,CD}}{2}\) |
|
|
\(\widehat {CMD} = \dfrac{{sd\,cung\,AB + sd\,cung\,CD}}{2}\) |
|
Advertisements (Quảng cáo)

|
Đẳng thức |
Diễn giải |
|
\(\)\(\widehat {AMB} = \widehat {ADB} + \widehat {CAD}\) |
Góc ngoài của \(\Delta AMD\) |
|
\(\widehat {ADB} = \dfrac{{sd\,cung\,AB}}{2}\) |
\(\widehat {ADB}\) là góc nội tiếp chắn cung AB |
|
\(\widehat {CAD} = \dfrac{{sd\,cung\,CD}}{2}\)\(\) |
\(\widehat {CAD}\) là góc nội tiếp chắn cung CD |
|
\(\widehat {AMB} = \dfrac{{sd\,cung\,AB + sd\,cung\,CD}}{2}\) |
Do \(\widehat {AMB} = \widehat {ADB} + \widehat {CAD} \Rightarrow \widehat {AMB} = \dfrac{{sd\,cung\,AB + sd\,cung\,CD}}{2}\) |
|
\(\widehat {CMD} = \dfrac{{sd\,cung\,AB + sd\,cung\,CD}}{2}\) |
Vì \(\widehat {AMB} = \widehat {CMD}\) (hai góc đối đỉnh) |
