a) Vẽ đồ thị các hàm số \(y = x\) và \(y = 2x + 2\) trên mặt phẳng tọa độ.
b) Gọi A là giao điểm của hai đồ thị nói trên, tìm tọa độ điểm A.
c) Vẽ qua điểm B(0; 2) một đường thẳng song song với trục Ox, cắt đường thẳng y = x tại điểm C. Tìm tọa độ của điểm C rồi tính diện tích tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét)

a) Đồ thị như hình bên.
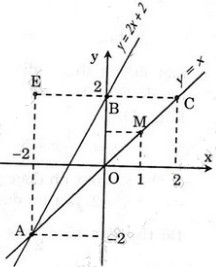
b) Giải phương trình hoành độ giao điểm: \(x = 2x + 2\), ta được \(x = -2 \Rightarrow y = -2\).
Vậy có tọa độ điểm A(-2; -2).
Advertisements (Quảng cáo)
c) C(2; 2).
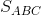 =
=  BC . 4 = 2 . 2 = 4 (cm2).
BC . 4 = 2 . 2 = 4 (cm2).
Vì điểm C là giao điểm của đường thẳng qua B và song song với trục hoành với hàm số \(y=x\) nên C là giao điểm của 2 hàm số sau:
\(\left\{\begin{matrix} y=x\\ y=2 \end{matrix}\right.\)
Vậy ta có tọa độ điểm \(C(2;2)\)
Diện tích của tam giác ABC là:
\(S_{ABC}=\frac{1}{2}BC.4=2BC=2.2=4(cm^2)\)
