a) Vẽ trên cùng hệ trục tọa độ Oxy đồ thị các hàm số sau:
y = x (d1) ;
y = 2x (d2);
y = -x + 3 (d3).
b) Đường thẳng (d3) cắt các đường thẳng (d1); (d2) theo thứ tự tại A, B.
Tìm tọa độ của các điểm A, B và tính diện tích tam giác OAB.

a) * Vẽ đồ thị của hàm số y = x
Cho x = 0 thì y = 0
Cho x = 1 thì y = 1
Đồ thị hàm số y = x là đường thẳng đi qua gốc tọa độ O(0;0) và điểm (1;1)
* Vẽ đồ thị của hàm số y = 2x
Cho x = 0 thì y = 0
Cho x = 1 thì y = 2
Đồ thị hàm số y = 2x là đường thẳng đi qua gốc tọa độ O(0;0) và điểm (1;2)
* Vẽ đồ thị của hàm số y = -x + 3
Cho x = 0 thì y = 3. Ta có điểm (0;3)
Advertisements (Quảng cáo)
Cho y = 0 thì x = 3. Ta có điểm (3;0)
Đồ thị hàm số y = -x + 3 là đường thẳng đi qua hai điểm (0;3) và điểm (3;0)
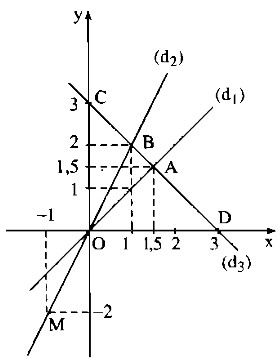
b) * Gọi \(A\left( {{x_1};{y_1}} \right),\,\,B\left( {{x_2};{y_2}} \right)\), lần lượt là tọa độ giao điểm của đường thẳng (d3) với hai đường thẳng (d1); (d2).
Ta có: A thộc đường thẳng y = x nên \({y_1} = {x_1}\)
A thuộc đường thẳng y = -x + 3 nên \({y_1} = - {x_1} + 3\)
Suy ra:
\(\eqalign{
& {x_1} = - {x_1} + 3 \cr
& \Leftrightarrow 2{x_1} = 3 \cr
& \Leftrightarrow {x_1} = 1,5 \cr} \)
\({x_1} = 1,5 \Rightarrow {y_1} = 1,5\)
Vậy tọa độ giao điểm của hai đường thẳng (d1) và (d2) là A(1,5;1,5).
Ta có: B thuộc đường thẳng y = 2x nên \({y_2} = 2{x_2}\)
B thuộc đường thẳng y = -x + 3 nên \({y_2} = - {x_2} + 3\)
Suy ra :
\(\eqalign{
& 2{x_2} = - {x_2} + 3 \cr
& \Leftrightarrow 3{x_2} = 3 \cr
& \Leftrightarrow {x_2} = 1 \cr} \)
\({x_2} = 1 \Rightarrow {y_2} = 2\)
Vậy tọa độ giao điểm của hai đường thẳng (d1) và (d2) là B(1;2).
