Trên hình 89 hai đường tròn tiếp xúc nhau tại A. Chứng minh rằng OC//O'D.. Bài 33 trang 119 sgk Toán 9 - tập 1 - Bài 7+8. Vị trí tương đối của hai đường tròn
Trên hình 89 hai đường tròn tiếp xúc nhau tại A. Chứng minh rằng OC//O’D.
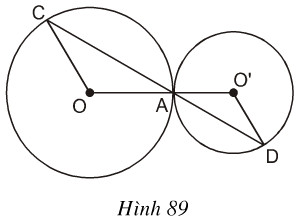

(O) và (O’) tiêó xúc nhau tại A (gt) ⇒ O,A, O’ thẳng hàng.
Advertisements (Quảng cáo)
∆OCA có OC = OA (= R) nên tam giác cân tại O
\( \Rightarrow \widehat {OAC} = \widehat {OC{\rm{A}}}\)
Tương tự có \(\widehat {O’A{\rm{D}}} = \widehat {O’DA}\) mà \(\widehat {OAC} = \widehat {O'{\rm{AD}}}\) (đối đỉnh)
Suy ra \(\widehat {OC{\rm{A}}} = \widehat {O’DA}\) mà góc \(\widehat {OC{\rm{A}}}\) và \(\widehat {O’D{\rm{A}}}\) so le trong, do đó OC // O’D (đpcm)
