Bài 39. Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, \(B\in (O),C\in (O’).\) Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC ở I.
a) Chứng minh rằng \(\widehat{BAC}=90^{\circ}\).
b) Tính số đo góc OIO’.
c) Tính độ dài BC, biết \(OA=9cm, O’A=4cm.\)

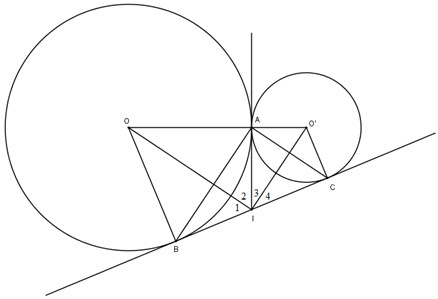
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có \(IA=IB=IC=\frac{1}{2}BC\).
Do đó tam giác ABC vuông tại A
Advertisements (Quảng cáo)
\(\Rightarrow \widehat{BAC}=90^{\circ}\).
b) Ta có \(\widehat{I}_{1}=\widehat{I}_{2};\widehat{I}_{3}=\widehat{I}_{4}\) (tính chất hai tiếp tuyến cắt nhau).
Do đó \(\widehat{OIO’}=90^{\circ}\) (hai tia phân giác của hai góc kề bù).
c) Ta có \(AI\perp OO’\).
Xét tam giác OIO’ vuông tại I, ta có:
\(IA^{2}=OA\cdot O’A=9\cdot 4=36\Rightarrow IA=6.\)
Do đó \(BC=12cm.\)
Nhận xét. Câu a), b) chỉ là gợi ý để làm câu c). Đối với những bài toán có hai đường tròn tiếp xúc, ta thường vẽ thêm tiếp tuyến chung tại tiếp điểm để xuất hiện yếu tố trung gian giúp cho việc tính toán hoặc chứng minh được thuận lợi.
