a) Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ:
y = 2x (1);
y = 0,5x (2);
y = -x + 6 (3)
b) Gọi các giao điểm của đường thẳng có phương trình (3) với hai đường thẳng có phương trình (1) và (2) theo thứ tự là A và B. Tìm tọa độ của hai điểm A và B.
c) Tính các góc của tam giác OAB.
Hướng dẫn câu c)
Tính OA, OB rồi chứng tỏ tam giác OAB là tam giác cân.
Tính \(\widehat {AOB} = \widehat {AOx} - \widehat {BOx}\)
Hướng dẫn làm bài:
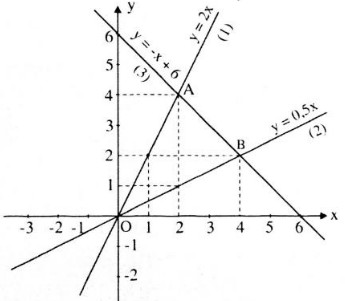
a) Đồ thị xem hình bên
b) Tìm tọa độ điểm A.
Advertisements (Quảng cáo)
-x + 6 = 2x ⇔ 6 = 2x + x ⇔ x = 3
x = 2 thì y = -2 + 6 = 4 nên A(2; 4)
Tìm tọa độ điểm B.
-x + 6 = 0,5x ⇔ 6 = 0,5x + x ⇔ x = 4
Với x = 4 thì y = -4 + 6 = 2 nên B(4;2)
c)
\(\eqalign{
& O{A^2} = {2^2} + {4^2} = 20 \Rightarrow OA = \sqrt {20} \cr
& O{B^2} = {4^2} + {2^2} = 20 \Rightarrow OB = \sqrt {20} \cr
& OA = OB\left( { = \sqrt {20} } \right) \cr} \)
⇒ ∆OAB cân tại O
Ta có \(tg\widehat {BOx} = {2 \over 4} = {1 \over 2} \Rightarrow \widehat {BOx} \approx {26^0}34’\)
và \(tg\widehat {AOx} = {4 \over 2} = 2 \Rightarrow \widehat {AOx} \approx {63^0}26’\)
Do đó \(\widehat {AOB} = \widehat {AOx} - \widehat {BOx} = {36^0}52’\)
Nên \(\widehat {OAB} = \widehat {OBA} \approx {{{{180}^0} - {{36}^0}52′} \over 2} = {71^0}34’\)
