Bài 64.Trên đường tròn bán kính \(R\) lần lượt đặt theo cùng một chiều, kể từ điểm \(A\), ba cung \(\overparen{AB}\), \(\overparen{BC}\), \(\overparen{CD}\) sao cho: \(sđ\overparen{AB}\)=\(60^0\), \(sđ\overparen{BC}\)=\(90^0\), \(sđ\overparen{CD}\)=\(120^0\)
a) Tứ giác \(ABCD\) là hình gì?
b) Chứng minh hai đường chéo của tứ giác \(ABCD\) vuông góc với nhau.
c) Tính độ dài các cạnh của tứ giác \(ABCD\) theo \(R\).
Hướng dẫn giải:
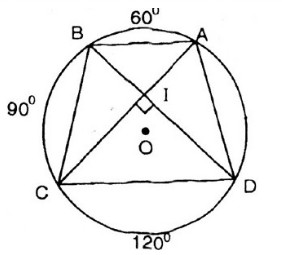
\(\widehat {BA{\rm{D}}} = {{{{90}^0} + {{120}^0}} \over 2} = {105^0}\) (góc nội tiếp chắn \(\overparen{BCD}\)) (1)
\(\widehat {A{\rm{D}}C} = {{{{60}^0} + {{90}^0}} \over 2} = {75^0}\) ( góc nội tiếp chắn\(\overparen{ABC}\) ) (2)
Từ (1) và (2) có:
\(\widehat {BA{\rm{D}}} + \widehat {A{\rm{D}}C} = {105^0} + {75^0} = {180^0}\) (3)
\(\widehat {BA{\rm{D}}}\) và \(\widehat {A{\rm{D}}C}\) là hai góc trong cùng phía tạo bởi cát tuyến \(AD\) và hai đường thẳng \(AB, CD\).
Advertisements (Quảng cáo)
Đẳng thức (3) chứng tỏ \(AB // CD\). Do đó tứ giác \(ABCD\) là hình thang, mà hình thang nội tiếp là hình thang cân.
Vậy \(ABCD\) là hình thang cân (\(BC = AD\) và \(sđ\overparen{BC}\)=\(sđ\overparen{AD}\)=\(90^0\))
b) Giả sử hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(I\).
\(\widehat {CI{\rm{D}}}\) là góc có đỉnh nằm trong đường tròn, nên:
\(\widehat {CI{\rm{D}}}\) = \(\frac{sđ\overparen{AB}+sđ\overparen{CD}}{2}\)=\({{{{60}^0} + {{120}^0}} \over 2} = {90^0}\)
Vậy \(AC \bot BD\)
c)
Vì \(sđ\overparen{AB}\) = \(60^0\) nên \(\widehat {AIB} = {60^0}\) \(=> ∆AIB\) đều, nên \(AB = R\)
Vì \(sđ\overparen{BC}\)= \(90^0\) nên \(BC = R\sqrt2\)
\( AD = BC = R\sqrt2\)
nên \(sđ\overparen{CD}\)= \(120^0\) nên \(CD = R\sqrt3\)
