Bài 95. Các đường cao hạ từ \(A\) và \(B\) của tam giác \(ABC\) cắt nhau tại \(H\) (góc \(C\) khác \(90^0\)) và cắt đường tròn ngoại tiếp tam giác \(ABC\) lần lượt tại \(D\) và \(E\). Chứng minh rằng:
a) \(CD = CE\) ; b) \(ΔBHD\) cân ; c) \(CD = CH\).

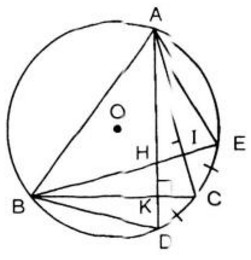
Ta có: \(\widehat {A{\rm{D}}B} = \widehat {A{\rm{E}}B}\) (cùng chắn cung \(AB\))
\( \Rightarrow \widehat {CB{\rm{D}}} = \widehat {CA{\rm{E}}}\) (cùng phụ với hai góc bằng nhau)
⇒ \(sđ\overparen{CD}\)= \(sđ\overparen{CE}\)
Advertisements (Quảng cáo)
Suy ra \(CD = CE\)
b) Ta có \(\widehat {EBC}\) và \(\widehat {CB{\rm{D}}}\) là góc nội tiếp trong đường tròn \(O\) nên :
\(\widehat {EBC} = {1 \over 2} sđ\overparen{CE}\) và \(\widehat {CB{\rm{D}}} = {1 \over 2}sđ\overparen{CD}\)
Mà \(sđ\overparen{CD}\)= \(sđ\overparen{CE}\)
nên \(\widehat {EBC} = \widehat {CB{\rm{D}}}\)
Vậy \(∆BHD\) cân tại \(B\)
c) Vì \(∆BHD\) cân và \(BK\) là đường cao cũng là đường trung trực của \(HD\). Điểm \(C\) nằm trên đường trung trực của \(HD\) nên \(CH = CD\)
