Bài 97. Cho tam giác \(ABC\) vuông ở \(A\). Trên \(AC\) lấy một điểm \(M\) và vẽ đường tròn đường kính \(MC\). Kẻ \(BM\) cắt đường tròn tại \(D\). Đường thẳng \(DA\) cắt đường tròn tại \(S\). Chứng minh rằng:
a) \(ABCD\) là một tứ giác nội tiếp;
b) \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{D}}}\) ;
c) \(CA\) là tia phân giác của góc \(SCB\)

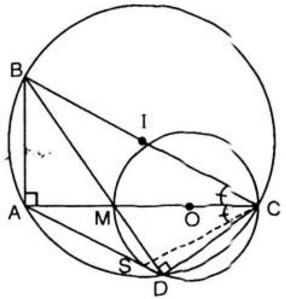
a) Ta có góc \(\widehat {MDC}\) là góc nội tiếp chắn nửa đường tròn \((O)\) nên \(\widehat {MDC} = {90^0}\)
⇒ \(∆CDB\) là tam giác vuông nên nội tiếp đường tròn đường kính \(BC\) .
Ta có \(∆ABC\) vuông tại \(A\).
Do đó \(∆ABC\) nội tiếp trong đường tròn tâm \(I\) đường kính \(BC\).
Advertisements (Quảng cáo)
Ta có \(A\) và \(D\) cùng nhìn \(BC\) dưới một góc \(90^0\) không đổi nên tứ giác \(ABCD\) nội tiếp đường tròn đường kính \(BC\)
b) Ta có \(\widehat {AB{\rm{D}}}\) là góc nội tiếp trong đường tròn \((I)\) chắn cung \(AD\).
Tương tự góc \(\widehat {AC{\rm{D}}}\) là góc nội tiếp trong đường tròn \((I)\) chắn cung \(AD\)
Vậy \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{D}}}\)
c) Ta có:
\(\widehat {S{\rm{D}}M} = \widehat {SCM}\) (vì góc nội tiếp cùng chắn cung \(MS\) của đường tròn \((O)\))
\(\widehat {A{\rm{D}}B} = \widehat {ACB}\) (là góc nội tiếp cùng chắn cung \(AB\) của đường tròn \((I)\)
Mà \(\widehat {A{\rm{D}}B} = \widehat {S{\rm{D}}M} \Rightarrow \widehat {SCM} = \widehat {ACB}\)
Vậy tia \(CA\) là tia phân giác của góc \(SCB\)
