Câu hỏi/bài tập:
Cho tam giác ABC \(\left( {AB < AC} \right)\) ngoại tiếp đường tròn (I) với các tiếp điểm BC, CA, AB lần lượt là D, E, F. Gọi X và Y lần lượt là chân đường cao kẻ từ B và C xuống CI và BI. Chứng minh rằng:
a) DBXF, DCYE là các tứ giác nội tiếp.
b) Bốn điểm X, Y, E, F thẳng hàng.
a) Vì \(\widehat {IXB} = \widehat {IDB} = \widehat {IFB} = {90^0}\) và \(\widehat {IYC} = \widehat {IDC} = \widehat {IEC} = {90^0}\) nên \(D,B,X,F,I\) cùng thuộc một đường tròn và \(D,C,Y,E,I\) cùng thuộc một đường tròn. Suy ra DBXF và DCYE là các tứ giác nội tiếp.
b) + \(\widehat {IXB} = \widehat {IYC} = {90^0}\) nên BXYC là tứ giác nội tiếp. Suy ra \(\widehat {YXC} = \widehat {YBC} = \widehat {IBF} = \widehat {IXF}.\) Suy ra X, F, Y thẳng hàng.
+ Chứng minh tương tự ta có X, E, Y thẳng hàng. Vậy ta có X, E, F, Y thẳng hàng
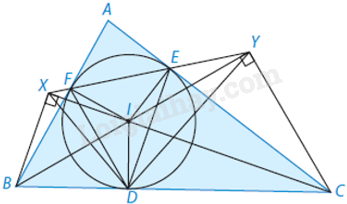
a) Ta có \(\widehat {IXB} = \widehat {IDB} = \widehat {IFB} = {90^0}\) và \(\widehat {IYC} = \widehat {IDC} = \widehat {IEC} = {90^0}\) nên \(D,B,X,F,I\) cùng thuộc một đường tròn và \(D,C,Y,E,I\) cùng thuộc một đường tròn. Suy ra DBXF và DCYE là các tứ giác nội tiếp.
b) Ta có \(\widehat {IXB} = \widehat {IYC} = {90^0}\) nên BXYC là tứ giác nội tiếp. Suy ra \(\widehat {YXC} = \widehat {YBC} = \widehat {IBF} = \widehat {IXF}.\)
Nên X, F, Y thẳng hàng. Tương tự X, E, Y thẳng hàng. Vậy ta có X, F, E, Y thẳng hàng.