Câu hỏi/bài tập:

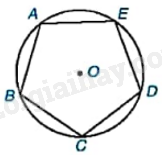
Cho ngũ giác đều ABCDE nội tiếp đường tròn (O) như hình bên.
a) Hãy tìm một phép quay thuận chiều tâm O biến điểm A thành điểm C.
b) Phép quay trên sẽ biến các điểm B, C, D, E lần lượt thành những điểm nào? Phép quay này có giữ nguyên ngũ giác đều ABCDE không?

+ Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
Advertisements (Quảng cáo)
+ Một phép quay được gọi là giữ nguyên một đa giác đều H nếu phép quay đó biến mỗi điểm của H thành một điểm của H.

a) Ta thấy \(\widehat {AOC} = \frac{2}{5}{.360^ \circ } = {144^ \circ }\).
Vậy phép quay ngược chiều \({144^{\rm{o}}}\) tâm O biến điểm \(A\) thành điểm \(C\)
b) Phép quay trên lần lượt biến \(B,C,D,E\) thành \(D,E,A,B\).
Như vậy phép quay này biến các đỉnh của ngũ giác đều \(ABCDE\) thành các đỉnh của chính nó.
Do vậy phép quay này giữ nguyên ngũ giác đều \(ABCDE\).
