Câu hỏi/bài tập:

Cho tam giác ABC nhọn có trực tâm H và nội tiếp đường tròn (O). Lấy D là điểm đối xứng với A qua O. Chứng minh rằng DH đi qua trung điểm BC.

+ Chứng minh \(\widehat {ABD} = \widehat {ACD} = {90^o}\) hay \(BD \bot AB,DC \bot AC\).
+ Chứng minh \(HC \bot AB,HB \bot AC\). Từ đó chứng minh được BH//DC; HC//BD.
Advertisements (Quảng cáo)
+ Chứng minh BDCH là hình bình hành nên DH đi qua trung điểm BC.

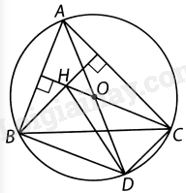
Vì AD là đường kính của (O) nên \(\widehat {ABD}\) và \(\widehat {ACD}\) là các góc nội tiếp của (O) chắn nửa đường tròn. Do đó, \(\widehat {ABD} = \widehat {ACD} = {90^o}\), hay \(BD \bot AB,DC \bot AC\). (1)
Mặt khác, vì H là trực tâm của tam giác ABC nên \(HB \bot AC,HC \bot AB\). (2).
Từ (1) và (2), ta suy ra BH//DC; HC//BD. Do đó, BDCH là hình bình hành. Vì vậy DH và BC cắt nhau tại trung điểm của mỗi đoạn thẳng.
