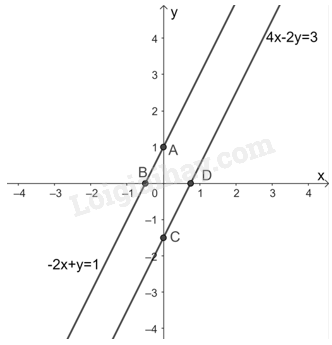
Cho hệ phương trình (I) \(\left\{ \begin{array}{l} - 2x + y = 1\\4x - 2y = 3\end{array} \right.\).
a) Giải hệ phương trình (I).
b) Vẽ hai đường thẳng \( - 2x + y = 1\) và \(4x - 2y = 3\) trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu a.

a) Giải phương trình bằng phương pháp cộng đại số.
b) Cách vẽ đường thẳng trên mặt phẳng tọa độ:
+ Xác định tọa độ hai điểm thuộc đường thẳng đó.
Advertisements (Quảng cáo)
+ Vẽ đường thẳng đi qua hai điểm đó ta được đường thẳng cần tìm.

a) Nhân hai vế phương trình thứ nhất với 2, ta được hệ phương trình \(\left\{ \begin{array}{l} - 4x + 2y = 2\\4x - 2y = 3\end{array} \right.\).
Cộng từng vế hai phương trình của hệ mới, ta được \(0x + 0y = 5\).
Do không có giá trị nào của x và y thỏa mãn hệ thức trên nên hệ phương trình đã cho vô nghiệm.
b)