Câu hỏi/bài tập:

Cho tam giác nhọn ABC có các đường cao BE, CF cắt nhau tại H. Chứng minh rằng:
a) \(\widehat {EFH} = \widehat {HBC},\widehat {FEH} = \widehat {HCB}\);
b) \(\widehat {BHF} = \widehat {BAC} = \widehat {CHE}\).

a) + Chứng minh các tam giác vuông BFC và BEC cùng nội tiếp đường tròn đường kính BC nên tứ giác BCEF nội tiếp đường tròn đường kính BC. Từ đó suy ra \(\widehat {EFC} = \widehat {EBC}\).
+ Chứng minh tương tự ta có: \(\widehat {FEH} = \widehat {HCB}\).
b) + Chứng minh các tam giác vuông AEH và AFH cùng nội tiếp đường tròn đường kính AH nên tứ giác AEHF nội tiếp đường tròn đường kính AH.
+ Chứng minh \(\widehat {EHF} + \widehat {EAF} = {180^o}\), suy ra \(\widehat {BHF} = {180^o} - \widehat {EHF} = \widehat {EAF} = \widehat {BAC}\).
+ Chứng minh tương tự ta có: \(\widehat {CHE} = \widehat {BAC}\).
Advertisements (Quảng cáo)

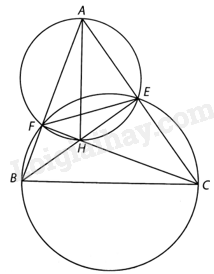
a) Ta có: \(\widehat {BFC} = \widehat {BEC} = {90^o}\). Do vậy các tam giác vuông BFC và BEC cùng nội tiếp đường tròn đường kính BC.
Suy ra, tứ giác BCEF nội tiếp đường tròn đường kính BC. Vì \(\widehat {EFC}\) và \(\widehat {EBC}\) là hai góc nội tiếp đường tròn ngoại tiếp của tứ giác này và cùng chắn cung CE nên \(\widehat {EFC} = \widehat {EBC}\). Suy ra \(\widehat {EFH} = \widehat {EFC} = \widehat {EBC} = \widehat {HBC}\).
Tương tự ta có: \(\widehat {FEH} = \widehat {HCB}\).
b) Ta có: \(\widehat {AEH} = \widehat {AFH} = {90^o}\). Do vậy các tam giác vuông AEH và AFH cùng nội tiếp đường tròn đường kính AH.
Suy ra, tứ giác AEHF nội tiếp đường tròn đường kính AH. Vì góc FAE và góc FHE là hai góc đối của tứ giác nội tiếp AEHF nên \(\widehat {EHF} + \widehat {EAF} = {180^o}\).
Suy ra \(\widehat {BHF} = {180^o} - \widehat {EHF} = \widehat {EAF} = \widehat {BAC}\).
Tương tự ta có: \(\widehat {CHE} = \widehat {BAC}\).
Vậy \(\widehat {BHF} = \widehat {BAC} = \widehat {CHE}\).
